Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 9º ano do Ensino Fundamental.

Disponível em: <Flecha Definir Linha – Gráfico vetorial grátis no Pixabay> Acesso em: 25 de agosto de 2022.
A proporcionalidade direta e a proporcionalidade inversa são dois conceitos fundamentais na matemática que descrevem relações entre duas quantidades. Essas relações são importantes para entender como uma quantidade varia em relação à outra e podem ser aplicadas em uma variedade de situações do mundo real.
A proporcionalidade direta ocorre quando duas quantidades aumentam ou diminuem na mesma proporção. Isso significa que, à medida que uma quantidade aumenta, a outra também aumenta na mesma taxa, e quando uma quantidade diminui, a outra também diminui na mesma taxa. Podemos representar essa relação usando a fórmula geral y = kx, onde y e x são as quantidades variáveis e k é uma constante de proporcionalidade. Essa constante indica o fator pelo qual as quantidades estão relacionadas entre si. Por exemplo, se estamos considerando a relação entre o número de horas trabalhadas e o salário recebido, na proporcionalidade direta, se dobrarmos o número de horas trabalhadas, o salário também dobrará.
Já a proporcionalidade inversa ocorre quando duas quantidades têm uma relação inversa entre si. Isso significa que, à medida que uma quantidade aumenta, a outra diminui na mesma proporção, e vice-versa. Podemos representar essa relação usando a fórmula geral y = k / x, onde y e x são as quantidades variáveis e k é uma constante de proporcionalidade. Nesse caso, quando x aumenta em um determinado fator, y diminui na mesma proporção. Por exemplo, se estamos considerando a relação entre a velocidade média de um veículo e o tempo necessário para percorrer uma certa distância, na proporcionalidade inversa, se aumentarmos a velocidade do veículo, o tempo necessário para percorrer a distância diminuirá.
Esses conceitos de proporcionalidade direta e inversa são amplamente utilizados em várias áreas, como física, economia, engenharia e ciências naturais. Eles nos permitem compreender as relações entre diferentes variáveis e realizar cálculos e previsões com base nessas relações. Veja alguns exemplos de exercícios resolvidos:
Problema: Um carro percorre 300 km em 4 horas. Se mantiver a mesma velocidade constante, quantos quilômetros ele percorrerá em 8 horas?
Solução: Neste caso, a velocidade do carro é constante, o que significa que há uma relação de proporcionalidade direta entre a distância percorrida e o tempo.
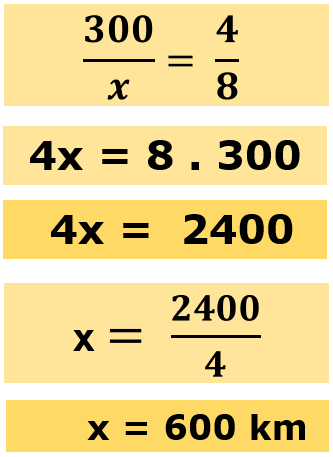
Então, ele percorrerá 8 km em 8 horas.
Problema: Um trabalho pode ser realizado por 6 operários em 9 dias. Quantos operários são necessários para realizar o mesmo trabalho em 3 dias?
Solução: Neste caso, há uma relação de proporcionalidade inversa entre o número de operários e o tempo necessário para realizar o trabalho.
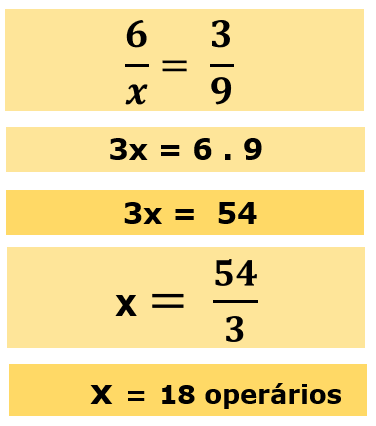
Então, serão necessários 18 operários.
Assista a videoaula da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
O rótulo de um produto de limpeza recomenda a diluição de 20 mL em 1 litro de água.

Disponível em: <Limpeza Equipamento Spray Limpando – Foto gratuita no Pixabay> Acesso em 01 de agosto de 2022.
a) Qual a razão entre essas grandezas?
b) Se desejar usar 50 mL do produto mantendo a diluição recomendada pelo rótulo, quanto de água será necessário?
Questão 2
Trabalhando 8 horas por dia, um pedreiro conclui uma obra em 150 dias. Se ele trabalhar 6 horas por dia quanto tempo levará para terminar essa obra?
(A) 200 dias
(B) 100 dias
(C) 225 dias
(D) 180 dias
Questão 3
Um medicamento tem a concentração de 5 mg a cada 2 gotas. Uma pessoa que precise de 125 mg desse medicamento usará quantas gotas?
(A) 50 gotas
(B) 60 gotas
(C) 62 gotas
(D) 65 gotas
Questão 4
Determine o valor de x para que a proporcionalidade seja verdadeira:
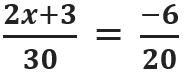
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF07MA17-A) Ler, interpretar, resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, para calcular a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros. (EF07MA17-B) Ler, interpretar, resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas. (EF08MA13) Ler, interpretar, resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas. |
| Descritores: | D29 – Resolver problema que envolva variações proporcionais, diretas ou inversas entre grandezas |
