Esta atividade tem como base as sequências didáticas propostas pelo Programa Aprender Sempre, da SME-Goiânia, com base no DC/GO – Ampliado e está destinada a estudantes do 8º ano do Ensino Fundamental.

Disponível em: <Torre De Transmissão – Foto gratuita no Pixabay> acesso em 01 de agosto de 2022
As figuras geométricas planas são elementos básicos da geometria, que nos permitem estudar e descrever formas e objetos no plano. A compreensão dessas figuras e de suas propriedades é essencial para o desenvolvimento do raciocínio espacial, da resolução de problemas e do pensamento matemático em geral.
O quadrado é uma figura plana que têm quatro lados iguais e quatro ângulos de 90º. A área de um quadrado é calculada elevando a medida do seu lado ao quadrado e o perímetro é quatro vezes o valor do lado. O triângulo é uma figura geométrica plana com 3 lados e é muito usada para dar estabilidade e melhorar a sustentação de construções da engenharia.
Ao analisar as mudanças no perímetro de um quadrado quando seus lados são ampliados ou reduzidos igualmente, podemos observar que o perímetro é proporcional à medida do lado. Isso significa que se aumentarmos ou diminuirmos a medida de todos os lados do quadrado na mesma proporção, o perímetro também será aumentado ou diminuído na mesma proporção. Por exemplo, se dobrarmos o comprimento de cada lado de um quadrado, seu perímetro será multiplicado por dois. Essa relação proporcional entre o perímetro e a medida do lado é uma propriedade dos quadrados.
No entanto, ao considerar a área de um quadrado, as coisas são diferentes. A área de um quadrado é determinada pelo produto da medida de um lado pelo mesmo lado. Se ampliarmos ou reduzirmos igualmente a medida dos lados de um quadrado, a área resultante será ampliada ou reduzida pela multiplicação do fator de escala ao quadrado. Por exemplo, se dobrarmos o comprimento de cada lado de um quadrado, sua área será multiplicada por quatro. Isso ocorre porque a área depende do produto das medidas dos lados, enquanto o perímetro depende apenas das medidas dos lados.
Para calcular área de variadas figuras geométricas planas podemos decompor essas figuras em formas mais simples, como quadrados, retângulos e triângulos, e calcular a área de cada uma dessas formas separadamente. Em seguida, somamos as áreas das formas individuais para obter a área total da figura. Essa abordagem permite que lidemos com figuras complexas e irregulares de forma mais simples, dividindo-as em partes conhecidas e calculando suas áreas separadamente.
Assista a videoaula abaixo da professora Priscilla com essa temática.
VAMOS RESPONDER ALGUMAS QUESTÕES?
Questão 1
O tangram é um quebra-cabeça chinês construído com 7 peças: um quadrado, dois triângulos grandes, um triângulo médio, dois triângulos pequenos e um paralelogramo. Com ele podem ser construídas diversas formas:

Disponível em: < Quebra-Cabeça Chinês Tangram – Gráfico vetorial grátis no Pixabay > Acesso em: 01 de agosto de 2022
Levando em consideração que esse tangram foi construído com os lados do quadrado medindo 4 cm responda:
- Qual a área desse quadrado?
- Observe que juntando dois triângulos pequenos formamos um quadrado. Qual seria então a área de cada um desses triângulos?
- Levando em consideração que a área do paralelogramo é igual a área do quadrado, qual seria a área total da casinha formada?
Questão 2
Aline desenhou em sua sala um mural com 20 quadradinhos iguais. A área pintada de cinza mede 8 cm2. Quanto mede a área branca?

Imagem do arquivo pessoal
(A) 8 cm2
(B) 10 cm2
(C) 12 cm2
(D)14 cm2
Questão 3
A figura a seguir, típica em um projeto de engenharia, mostra a planta baixa de uma kitnet e sua representação em 3D. As medidas do quarto e do banheiro estão especificadas no desenho. Levando em consideração um espaço de aproximadamente 1 metro para as aberturas das portas, responda:
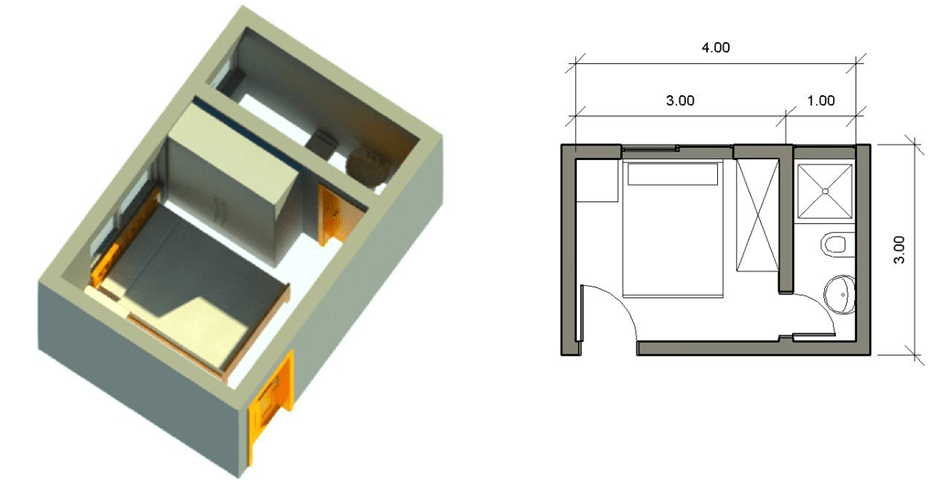
Imagem do arquivo pessoal
- Quantos metros de parede serão construídos ao todo nesse projeto?
- Sabendo que cada metro construído terá um custo aproximado de 5 reais, qual será o valor total gasto com as paredes?
Questão 4
Pedro separou uma área quadrada no seu terreno para fazer uma horta. Inicialmente ele pensou em fazer com 3 metros de lado, mas depois percebeu que essa área não era suficiente, e que o lado do quadrado deveria ter o dobro do tamanho para plantar todas as hortaliças. De quantos metros quadrados foi o aumento da área dessa região da horta?
(A) 36 metros quadrados.
(B) 27 metros quadrados.
(C) 25 metros quadrados.
(D) 16 metros quadrados.
| Autoria: | Priscilla Nascimento Dias, licenciada em matemática e pedagoga. |
| Componente Curricular: | Matemática |
| Habilidades: | (EF06MA29) Analisar e descrever mudanças que ocorrem no perímetro e na área de um quadrado ao se ampliarem ou reduzirem, igualmente, as medidas de seus lados, para compreender que o perímetro é proporcional à medida do lado, o que não ocorre com a área. (EF07MA32) Resolver e elaborar situações problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas. (EF06MA29) Analisar e descrever mudanças que ocorrem no perímetro e na área de um quadrado ao se ampliarem ou reduzirem, igualmente, as medidas de seus lados, para compreender que o perímetro é proporcional à medida do lado, o que não ocorre com a área. (EF07MA32) Resolver e elaborar situações problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas. |
| Descritores: | D5 – Reconhecer a conservação ou modificação de medidas dos lados, do perímetro, da área em ampliação e/ou redução de figuras poligonais usando malhas quadriculadas D12 – Resolver problema envolvendo o cálculo de perímetro de figuras planas D13 – Resolver problema envolvendo o cálculo de área de figuras planas |
