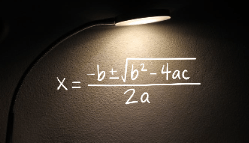Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 6º Período (8ª Série) da Educação de Jovens e Adultos – EJA
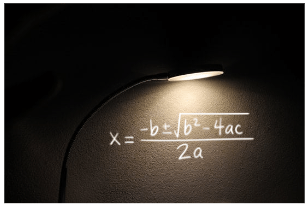
O que são equações?
As equações são expressões matemáticas que estabelecem uma igualdade entre duas informações. São compostas por variáveis (representadas por letras do nosso alfabeto), constantes (números reais), coeficientes (números reais) e um sinal de igualdade. Elas se diferem pelo valor do maior expoente das variáveis.
Imagem: canva.com/sombra_equação_https://encurtador.com.br/eoxP6
As equações do 2° grau com uma variável
As equações do segundo grau com uma variável são aquelas em que o maior expoente da variável é igual a 2. Elas possuem a seguinte forma geral:
ax2 + bx + c = 0
- x é a variável.
- a, b e c são os coeficientes, com a≠0
Como resolver uma equação do 2° grau?
A solução de uma equação do 2º grau (denominada de raiz da equação) é dada pelos valores da variável (x) que satisfazem a igualdade.
Existem alguns métodos para determinar essa solução, neste texto iremos apresentar o método que se utiliza da FÓRMULA RESOLUTIVA, mais conhecida como FÓRMULA DE BHASKARA.
Método da Fórmula Resolutiva (Fórmula de Bhaskara)
A solução de uma equação do 2° grau ax2 + bx + c = 0 pode ser encontrada pela fórmula:
Esta fórmula se utiliza dos coeficientes a, b e c.
O termo b2 – 4.a.c será denominado de discriminante (representado pela letra grega Δ), este termo irá indicar o número de raízes que terá a equação, ou seja:
Se Δ>0, a equação terá 2 raízes reais diferentes.
Se Δ<0, a equação não terá raízes reais.
Se Δ=0, a equação terá 2 raízes reais iguais, ou simplesmente, 1 raiz real.
Três exemplos para finalizar
Exemplo 1:
Determinar a solução da equação do 2º grau x2 – 9x + 14 = 0.
1º Passo: Destacar os coeficientes.
a = 1, b = – 9 e c = 14
2° Passo: Determinar o valor do discriminante e verificar o número de raízes.
Δ = b2 – 4 . a . c = (-9)2 – 4.1.14 = 81 – 56 = 25
Como Δ é maior do que zero, a equação terá 2 raízes reais e diferentes.
3º Passo: Determinar as raízes (solução)
Utilizando a fórmula de Bhaskara e indicando as raízes por x1 e x2 teremos:
Exemplo 2:
Determinar a solução da equação do 2º grau x2 + 5x + 8 = 0.
1º Passo: Destacar os coeficientes.
a = 1, b = 5 e c = 8
2° Passo: Determinar o valor do discriminante e verificar o número de raízes.
Δ = b2 – 4 . a . c = 52 – 4.1.8 = 25 – 32 = – 7
Como Δ é menor do que zero, a equação não terá raízes reais.
Neste caso, a solução será um conjunto vazio, representada por S = { } ou S =Ø.
Exemplo 3:
Determinar a solução da equação do 2º grau x2 + 8x + 16 = 0
1º Passo: Destacar os coeficientes.
a = 1, b = 8 e c = 16
2° Passo: Determinar o valor do discriminante e verificar o número de raízes.
Δ = b2 – 4 . a . c = 82 – 4.1.16 = 64 – 64 = 0
Como Δ é igual a zero, a equação terá 2 raízes reais e igual.
3º Passo: Determinar as raízes (solução)
Utilizando a fórmula de Bháskara e indicando as raízes por x1 e x2 teremos:
Neste caso não é necessário calcular o x2.
S = {-4,-4} ou S={-4}
Ficamos por aqui, até o próximo.
Questão 01
Um agricultor está planejando o layout de um campo retangular para cultivar duas variedades diferentes de plantas. A área total do campo é de 2400 metros quadrados. Ele deseja que o comprimento do campo seja 10 metros a mais que o dobro da largura. Qual deve ser a largura e o comprimento do campo? Veja a imagem ilustrando o problema.
Imagem do autor produzida no Geogebra
Questão 02
Determine a largura e o comprimento de um terreno com área de 30 metros quadrados e o comprimento medindo 3m a mais que a largura.
Imagem do autor produzida no Geogebra
Questão 03
Dada a equação quadrática 3x2 +7x−2=0, qual é a solução correta para x usando a fórmula de Bhaskara?
(A) x = 1
(B) x = -1
(C) x = 2
(D) x = -2
Questão 04
Considere a equação quadrática x2 – 6x + 8 = 0. Qual das seguintes opções representa corretamente as soluções para x usando a fórmula de Bhaskara?
(A) x=2 e x=4
(B) x=3 e x=5
(C) x=1 e x=8
(D) x=2 e x=8
SAIBA MAIS
Quer aprender um pouco mais sobre equações do 2º grau? Então assista aos vídeos no canal do YouTube do prof. Hélio
Como resolver equações do 2° grau completas
| Autoria | Prof. Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EAJAMA0810) Reconhecer uma equação do 2°grau, identificando seus coeficientes na forma completa (ax2 + bx + c = 0, a ≠ 0) e nas formas incompletas (ax2 + bx = 0, ax2 + c = 0, ax2 = 0 com a ≠ 0) quando apresentada em situações-problema, bem como determinar as suas raízes por meio da fatoração ou fórmula resolutiva. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 9° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018. |