Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 5º período (7ª série) da Educação de Jovens e Adultos – EJA.
Polígonos regulares
Os polígonos regulares são figuras em 2D (2 dimensões) que possuem todos os seus lados com o mesmo comprimento e todos os seus ângulos com a mesma medida. Os mais comuns são os triângulos equiláteros e os quadrados.
Imagem do autor produzida no Geogebra.
O Triângulo Equilátero
O triângulo equilátero é um tipo de triângulo que possui seus 3 lados com o mesmo comprimento e os seus 3 ângulos internos com a mesma medida.
Imagem do autor produzida no Geogebra
Como a soma dos ângulos internos de qualquer triângulo é igual a 180°, podemos afirmar que cada ângulo interno de um triângulo equilátero é igual a 60º (180º:3).
O Quadrado
O quadrado é um quadrilátero que possui os 4 lados com o mesmo comprimento e os 4 ângulos internos com a mesma medida.
Imagem do autor produzida no Geogebra
Como a soma dos ângulos internos de qualquer quadrilátero é igual a 360°, podemos afirmar que cada ângulo interno de um quadrado é igual a 90º (360º:4).
Ângulos externos de um triângulo equilátero e de um quadrado
Ângulo externo é o ângulo formado por um lado do polígono e a extensão de outro lado adjacente a ele.
Imagem do autor produzida no Geogebra
No triângulo POL, os ângulos x, y e z são ângulos externos e no quadrado RSTU, os ângulos r, s, t e u são ângulos externos.
Relação entre os ângulos internos e externos
A medida de um ângulo externo é suplementar do seu ângulo interno adjacente, ou seja, a soma de um ângulo externo com seu ângulo interno adjacente, é sempre igual a 180°.
Imagem do autor produzida no Geogebra
Dois problemas para finalizar
Problema 1
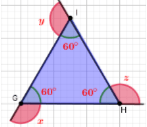
Dado um triângulo equilátero POL, onde todos os lados e ângulos são iguais, e cada ângulo interno mede 60o , determinar a medida de um ângulo externo.
Imagem do autor produzida no Geogebra
Solução:
Sabendo que a soma de um ângulo interno com seu ângulo externo adjacente é igual a 180°, teremos:
60° + y = 180° (Acrescentando – 60° no dois lados da equação)
y = 180º – 60°
y = 120°
Resposta: 120°.
OBS. Como todos os ângulos internos do triângulo equilátero é igual a 60º, podemos afirmar que todos os seus ângulos externos medem 120°.
Problema 1
Considere um quadrado RSTU com todos os lados e ângulos internos iguais. Sabendo que cada ângulo interno de um quadrado é 90o, determinar a medida de um ângulo externo.
Imagem do autor produzida no Geogebra
Solução:
Sabendo que a soma de um ângulo interno com seu ângulo externo adjacente é igual a 180°, teremos:
90° + a = 180° (Acrescentando – 90° no dois lados da equação)
y = 180º – 90°
y = 90°
Resposta: 90°.
OBS. Como todos os ângulos internos do quadrado é igual a 90º, podemos afirmar que todos os seus ângulos externos medem 90°.
Ficamos por aqui, até o próximo.
Questão 01
Calcule a soma das medidas dos ângulos externos m, n e p do triângulo equilátero ABC e x, y, z e w do quadrado IJKL.
Imagem do autor produzida no Geogebra
Questão 02
O polígono QRUST é composto por 1 triângulo equilátero e 1 quadrado. Determinar a soma das medidas dos seus ângulos internos.
Imagem do autor produzida no Geogebra
Questão 03
Sobre os ângulos internos e externos de um quadrado ABCD, podemos afirmar que:
(A) A soma dos seus ângulos internos é igual a 180º.
(B) Um dos seus ângulos externos mede 45º.
(C) Os seus ângulos internos medem 180º.
(D) A soma dos seus ângulos externos é igual a 360º.
Questão 04
Em um triângulo equilátero ABC, a medida de um ângulo interno é 60º, Se um dos ângulos externos desse triângulo for representado por xº, então o valor de de x é igual a:
(A) 30º.
(B) 60º.
(C) 90º.
(D) 120º.
SAIBA MAIS
Aprenda um pouco mais no canal do prof. Hélio: “Soma dos ângulos internos de um triângulo”.
| Autoria | Prof. Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular: | Matemática |
| Objetivos de Aprendizagem e Desenvolvimento: | (EJAMA0521) Calcular medidas de ângulos internos de polígonos regulares, e estabelecer relações entre ângulos internos e externos de polígonos (triângulo equilátero e quadrado). |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 8º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 8° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 8° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018. |
