Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes da 8ª Série da Educação de Jovens e Adultos – EJA.

Potenciação e radiciação
O que é potenciação e onde se aplica?
A potenciação é uma operação matemática que nos ajuda a simplificar cálculos repetitivos de multiplicação. Ela envolve um número chamado de base, que é multiplicado por ele mesmo várias vezes, determinado pelo expoente.
Imagem: canva.com/raiz e potenciação
É aplicada em diversas situações no nosso dia a dia, por exemplo no cálculo de áreas de terrenos, volume de objetos, cálculos de juros em investimentos, entre outras.
Como calcular a potenciação?
Por exemplo, quanto é 2 elevado a quarta potência?
Devemos multiplicar o 2, quatro vezes.

Certo, e como calcular 2 elevado a quarta potência negativa?
A potência com expoente negativo pode ser interpretada como o inverso da potência com expoente positivo correspondente.
É como se estivéssemos dividindo 1 pela potência positiva.
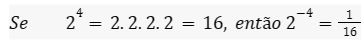
Então, para calcular a potência com expoente negativo, basta inverter o resultado dessa mesma potência com o expoente positivo.
Veja no saiba mais um vídeo explicativo.
E se a potência tiver um expoente fracionário, por exemplo, 5 elevado a 2/3?
Neste caso devemos transformá-la em uma radiciação, cuja definição está logo abaixo, ficando assim:
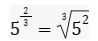
Observe que o denominador do expoente foi para o índice do radical e o numerador para o expoente.
Veja no saiba mais um vídeo explicativo.
O que é radiciação e onde se aplica?
A operação de radiciação é o oposto da operação de potenciação. Ela nos permite encontrar a raiz de um número, ou seja, o número que, elevado a um determinado expoente, resulta no número original.
É aplicada, principalmente, no cálculo de diagonais de retângulos e quadrados, em projetos de construção civil.
Como calcular a radiciação?
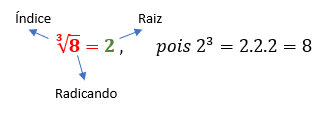
Por exemplo, quanto é a raiz cúbica de 8?
Como a radiciação é a operação inversa da potenciação, devemos encontrar um número que elevado ao cubo resulta 8, esse número é o 2.
Uma situação problema
João e Maria estão dividindo um bolo igualmente entre eles. No entanto, o bolo é dividido por 3 (uma situação diferente para ilustrar o tema) pedaços para cada um. João não está satisfeito com a presença da raiz no denominador e deseja racionalizar o denominador para facilitar a divisão igualitária. Ajude João.
Mas o que é racionalizar o denominador?
É um processo utilizado para tornar o denominador de uma fração mais simples e sem a presença de raízes no seu formato.
Neste caso multiplicamos o numerador e o denominador pela raiz quadrada de 3 e em seguida fazemos a multiplicação e extraímos a raiz quadrada de 9. Veja:
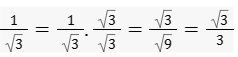
Observe que agora o denominador é um número inteiro.
Uma outra maneira de resolver a situação é usar o valor aproximado da raiz quadrada de 3 ( igual a 1,7) e em seguida fazer a divisão do bolo em 1,7 pedaços.
Ficamos por aqui, até o próximo.
Atividades
QUESTÃO 01
Uma população de bactérias duplica a cada hora. Se inicialmente havia 100 bactérias, o número de bactérias após 3 horas será de
(A) 50 bactérias.
(B) 200 bactérias.
(C) 300 bactérias.
(D) 800 bactérias.
QUESTÃO 02
Calcule o valor da expressão numérica abaixo:
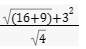
QUESTÃO 03
Uma caixa cúbica tem um volume de 64 metros cúbicos. Qual é a aresta dessa caixa? (Lembrando que aresta é o encontro das faces).
QUESTÃO 04
Uma empresa de eletrônicos está produzindo um novo modelo de smartphone com uma bateria de alta capacidade. Se a capacidade da bateria é de 5000 mAh (miliampere-hora) e a carga média consumida pelo smartphone a cada hora é de 250 mA, quantas horas o smartphone poderá ser utilizado continuamente antes de precisar ser recarregado?
(A) 10 horas.
(B) 15 horas.
(C) 20 horas.
(D) 25 horas.
SAIBA MAIS
Quer saber um pouco mais sobre potenciação? Assista aos vídeos no canal do Prof. Hélio
Expressão numérica com potenciação
Potência com expoente negativo
| Autoria | Prof. Hélio Roberto da Rocha, Mestre em Matemática |
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EAJAMA0804) Efetuar cálculos com números reais, inclusive com radicais e potenciação com expoente negativo e fracionário, usando propriedades operatórias, racionalização de denominadores, na resolução de situações problema diversos.(EAJAMA0805) Efetuar cálculos para aproximação de valores dos radicais que resultam em números irracionais. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018.GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. |

