Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes da 6ª Série da Educação de Jovens e Adultos – EJA.
Acesse essa proposta didática (slides 1 e atividade 1) em formato para impressão. Clique aqui: https://sme.goiania.go.gov.br/conexaoescola/propostas_didaticas/propostas-didatica-matematica-8a-serie/
A necessidade da existência de conjuntos numéricos surgiu a partir do momento que o homem necessitou de um método de contagem para representar quantidades. O primeiro conjunto numérico que surgiu foi o conjunto dos números naturais, cujos elementos representam grandezas inteiras e positivas. Tempos mais tarde algumas contagens não conseguiam mensurar algumas grandezas, como, por exemplo, um pedaço de um terreno, surgindo então o conjunto dos números racionais. Por volta do ano de 530 a.C., houve a necessidade de se mensurar a medida da diagonal de um quadrado e o comprimento de uma circunferência, surgindo então o conjunto dos números irracionais. Nesta atividade você irá trabalhar as operações que envolvem esses conjuntos.

Imagem: Pixabay.com.br
Questões propostas
QUESTÃO 01
Escreva as frações a seguir na forma de número decimal. Indique se a decimal é exata ou periódica e se for periódica, qual é o período?
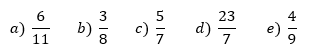
QUESTÃO 02
Escreva cada número decimal a seguir na forma de fração irredutível
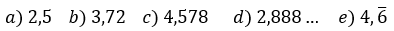
QUESTÃO 03
Na sequência, da esquerda para a direita, classifique os números em racionais ou irracionais.
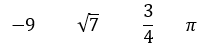
(a) Inteiro, irracional, racional e inteiro
(b) Racional, irracional, inteiro e racional
(c) Inteiro, racional, irracional e inteiro
(d) Racional, irracional, racional e irracional
QUESTÃO 04
Leia a receita abaixo

Classifique cada número dos ingredientes dessa receita em número natural, inteiro ou racional.
QUESTÃO 05
Escreva por extenso como se leem os números decimais abaixo e depois escreva-os na forma de fração irredutível.
(a) R$ 0,50
(b) 0,75 kg
(c) 0,238 litros
(d) 2,5m
(e) 4,58km
(f) R$ 2,3
QUESTÃO 06
Faça uma reta numérica e localize os números racionais abaixo.
a) 2,7
b) 1,5
c) -1,1
d) 7/4
e) 5/8
SAIBA MAIS
Para saber um pouco mais sobre conjuntos numéricos, assista aos vídeos abaixo do canal do Prof. Hélio
Questões da Prova Brasil envolvendo a reta numérica
Como determinar a fração geratriz de um número decimal periódico
Noções de números racionais
Noções de números irracionais
| Componente Curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EAJAMA0802) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero, localizando-os na reta numérica. |
| Referências | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 9º ano: ensino fundamental: anos finais / Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 9° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 9° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018 Site: A história dos conjuntos numéricos – URL https://www.partes.com.br/ |
