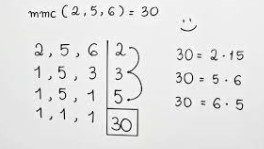Olá pessoal, a seguir será postado umas instruções sobre m.m.c. para tentar alcançar a compreensão dos discentes; leiam com atenção e depois faça as atividades.
Atividade 1
MÍNIMO MÚLTIPLO COMUM (MMC)
Os cálculos de MMC e MDC estão ligados aos múltiplos e aos divisores de um número. Esse tipo de cálculo, aprendido no ensino fundamental, é essencial para resolver muitas questões e problemas no Enem.
O mínimo múltiplo comum, ou MMC, de dois ou mais números inteiros é o menor múltiplo inteiro positivo comum a todos eles. Por exemplo, o MMC de 6 e 8 é o 24, e denotamos isso por mmc 6, 8 = 24 Já o MMC de 5, 6 e 8 é o 120, o que é denotado por MMC 5, 6, 8 = 120.
O MMC é muito útil quando se adicionam ou subtraem frações, pois é necessário um mesmo denominador comum durante esses processos. Não é necessário que esse denominador comum seja o MMC, mas a sua escolha minimiza os cálculos. Considere o exemplo:
326 + 18 = 656 + 756 = 1356, onde o denominador 56 foi usado porque MMC 28, 8 = 56.
Regra prática para calcular o MMC de dois números. Para calcular o MMC entre 28 e 8, fazemos o seguinte:
1. Reduzimos a fração 288 aos seus menores termos:
288 = 72.
2. Multiplicamos em cruz a expressão obtida:
28 x 2 = 8 x 7 = 56
3. O valor obtido é o MMC procurado: MMC 28, 8 = 56.
Regra geral para calcular o MMC de dois ou mais números. O procedimento geral para o cálculo do MMC envolve a decomposição primária de cada número. Por exemplo, para calcular o MMC de 8, 12 e 28, fazemos o seguinte:
1. Realizamos a decomposição primária de cada número:
8 = 23
12 = 22 ∙ 31
28 = 22 ∙ 71
2. Em seguida, multiplicamos cada fator primo elevado à maior potência com que aparece nas fatorações. O resultado é o MMC procurado:
MMC 8, 12, 28 = 23 ∙ 31 ∙ 71 = 168
Dispositivo prático para calcular o MMC de dois ou mais números. O procedimento acima tem a seguinte forma prática de execução:
1. Alinhamos os três números, 8, 12 e 28, e dividimos todos os números que podem ser divididos pelo primeiro primo 2. Na linha de baixo anotamos cada quociente obtido:
2. Repetimos esse procedimento sucessivamente com o 2, depois com o 3 e, depois com o 7, até que a última linha só contenha algarismos 1:
3. Agora, multiplicamos todos os fatores primos na coluna da direita, obtendo o MMC procurado:
MMC 8, 12, 28 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 7 = 168
Propriedade fundamental do MMC. Todo múltiplo comum de dois ou mais números inteiros é múltiplo do MMC destes números.
Exemplo: os múltiplos comuns positivos de 8, 12 e 28 são exatamente os múltiplos positivos de 168, o seu MMC, ou seja, são 168, 336, 504,…
Exemplo: encontre o menor número inteiro positivo de três algarismos que é divisível, ao mesmo tempo, por 3, 4 e 15.
Solução: pela propriedade fundamental do MMC, o número desejado será o menor número de três algarismos múltiplo do MMC de 3, 4 e 15. Como MMC 3, 4, 15 = 60, então o menor múltiplo de três algarismos é o 120.
Atividade 1 – Agora Copie e responda:
Questões:
2) Decompor em fatores primos os seguintes números:
a) 120 b) 135
c) 360 d) 900
03) Calcule o mínimo múltiplo comum (m.m.c.) entre os números dados em cada item:
a) 8 e 12
b) 12 e 36
c) 12 e 30
d) 24 e 30
e) 15 e 9
f) 12, 15 e 10
Atividade 2
Sua vez copie e responda.
Questões:
| Proponentes __Professores | VANDERLEY TAVARES DE MORAIS |
| Instituição Educacional | ESCOLA MUNICIPAL SÃO JOSÉ |
| CRE | Brasil di Ramos Caiado |
| EAJA | EAJA |
| EAJA – Série: | 6ª Série |
| Componente Curricular: | Língua Portuguesa |
| Habilidade estruturante Habilidades Complementares e Objetivos de Aprendizagem e Desenvolvimento | (EAJAMA0601) Resolver e elaborar situações problema com números naturais, envolvendo as noções de divisor e de múltiplo, incluindo os conceitos de máximo divisor comum ou mínimo múltiplo comum. OBJETIVOS: Apresentar aos discentes situações problemas que abordam m.m.c., bem como desenvolver neles habilidades para se encontrar o referido conceito (m.m.c.); Estimular os discentes a resolver problemas que envolvam m.m.c. |