Olá! Esta aula de Matemática é destinada aos educandos da 8ª Série da Eaja.
Nesta atividade você irá reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica e que pode ser escrita na forma de fração.
Assista à videoaula do professor Hélio Rocha com a temática números racionais.
Na vídeo aula, o professor Hélio Rocha explicou para você como os números racionais podem ser escritos. No entanto, para prosseguir a aula de hoje, você fará uma breve revisão dos conjuntos numéricos estudados até o momento. Combinado? Vamos lá!
Os números naturais: são todos os números inteiros não negativos e são agrupados em um conjunto numérico denominado de Conjunto dos Números Naturais indicado pela letra N.
N={0,1,2,3,4,5,6,…}
Os números inteiros: são todos os números inteiros negativos, positivos e nulo (zero). A reunião dos números naturais e dos números inteiros negativos forma o Conjunto dos Números Inteiros, indicado pela letra Z.
Z= {…, -3, -2, -1, 0, 1, 2, 3, …}
Os números racionais são todos aqueles que podem ser representados por uma fração a/b em que a e b são números inteiros quaisquer com b diferente de zero. Esses números são agrupados em um conjunto numérico chamado de Conjunto dos Números Racionais (Q).
Q = {a/b, com a e b números inteiros e b diferente de zero}.
Os números racionais podem ser organizados em dois grupos: o grupo dos racionais inteiros e o grupo dos racionais não inteiros.
Racionais inteiros: são todos os números inteiros positivos, negativos e nulo.
Exemplo: -8, 8, -7, 7, -4, 4, -1, 1, 0, …
Racionais não inteiros: são todos os números não inteiros positivos e negativos. Eles podem ser representados por uma fração cuja decimal pode ser exata ou periódica. Veja os exemplos a seguir.
Decimal exata

Veja os cálculos
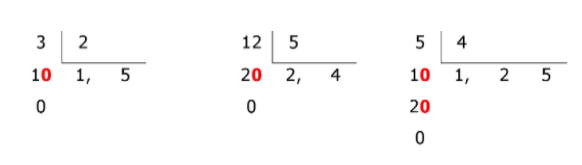
Decimal Periódica

Veja os cálculos
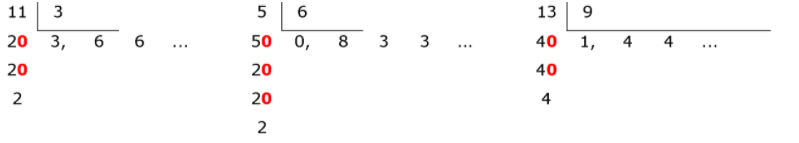
Na decimal periódica indicamos por PERÍODO o algarismo que se repete infinitamente. No caso da letra (a) o período é igual a 6, na letra (b) o período é igual a 3 e na letra (c) o período é igual a 4.
Como você percebeu, para escrever um número racional na forma de fração para a forma decimal, basta realizar a divisão. Se o resto for zero a decimal é chamada de DECIMAL EXATA e se o resto não for zero a decimal será chamada DECIMAL PERIÓDICA.
Veja o procedimento para transformar um número decimal para a forma de fração.
Exemplo 1 – Decimal Exata
A) 1. 2 – Esse caso é simples. Como temos 1 só algarismo na parte decimal, podemos escrever:
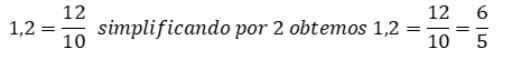
B) 2,35 – Como temos 2 algarismos na parte decimal, podemos escrever:

Exemplo 2 – Decimal Periódica com período composto por 1 algarismo. Para 2 ou mais algarismos pode-se fazer por analogia.
1,22222…. (Período 2)
Considere x = 1,2222…. (Equação 1)
Multiplicamos os dois membros por 10. A vírgula se desloca uma casa para a direita.
10.x = 12,222… (Equação 2)
Subtraindo (1) de (2) obtemos
9x = 11 Dividindo ambos os membros por 9, obtemos:
X = 11/9
Portanto 1,2222… = 11/9
Faça a prova fazendo a divisão de 11 por 9.
Caso tenha um algarismo antes do período e do lado direito da vírgula, como devo proceder? Veja o exemplo (b)
3,155555… (Período 5)
Considere x = 3,155555…
Multiplicando os dois membros por 10
10.x = 31,55555… (Equação 1)
Multiplicando novamente os dois membros por 10
100.x = 315,555… (Equação 2)
Subtraindo (1) de (2):
90.x = 284 Dividindo ambos os membros por 90 obtemos
x = 284/90 simplificando por 2 obtemos x = 142/45
Portando 3,15555… = 142/45
Faça a prova fazendo a divisão de 142 por 45 ou 284 por 90.
Todos esses números estudados até aqui, fazem parte do Conjunto dos Números Reais. Nas próximas atividades vamos estudar mais um subconjunto dos números reais, o Conjunto dos Números Irracionais.
Atividade 1
Transforme o número racional na forma de número decimal para a forma de fração.
1,225
Atividade 2
Escreva as frações apresentadas a seguir na forma de número decimal.
5/12
18/4
31/25
26/18
Atividade 3
Escreva cada número decimal a seguir na forma de fração irredutível.
4,16
3,6666….
1,85
1,25
Chegamos ao final de mais uma aula. Até a próxima e continue se cuidando!
| Referencia | Sousa, Joamir Roberto de – Matemática realidade & tecnologia: 9º ano. |
| Componente Curricular | Objeto de aprendizagem e desenvolvimento |
| Matemática | (EAJAMA0802) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).

