Noções de Função
OI, BOM DIA! ESPERO QUE ESTEJA SE CUIDANDO!! VAMOS CONTINUAR CONHECENDO A APLICAÇÃO DO PLANO CARTESIANO EM NOSSO COTIDIANO E RELACIONANDO ELA COM O ESPAÇO QUE VIVEMOS.
ATIVIDADE 1
Leia, atentamente, as seguintes situações:
1ª SITUAÇÃO:
Um estacionamento cobra a primeira hora, o valor de 7 reais e as demais horas excedentes R$ 2,00. Logo, o valor a ser pago, ao final, depende do número de horas em que o carro ficará estacionado

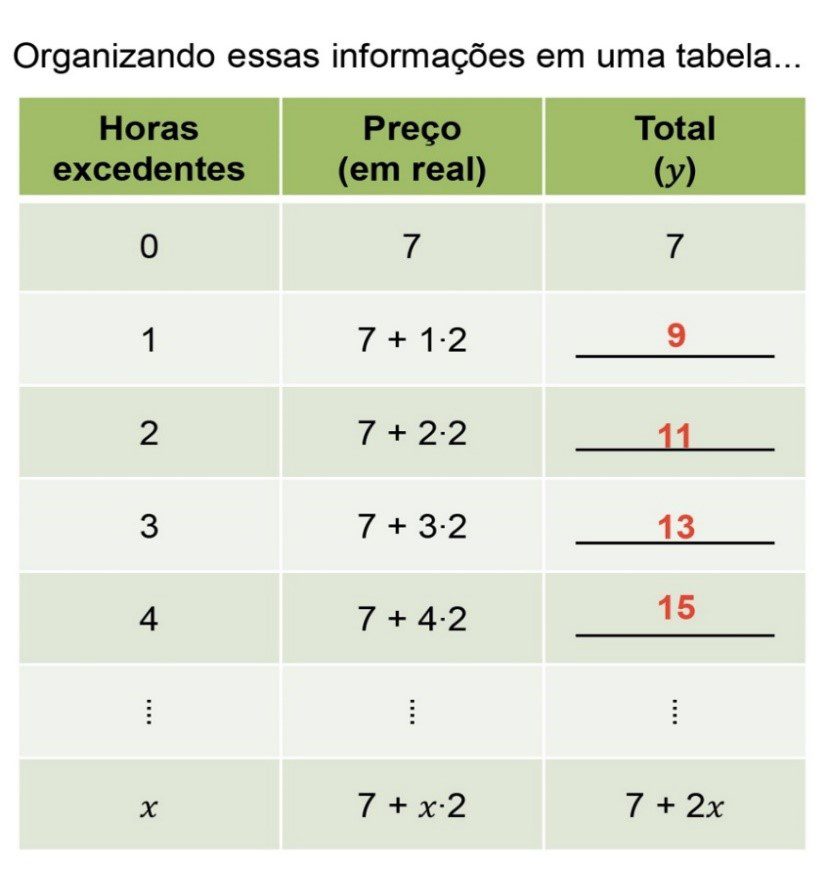
EXPLICAÇÃO:
Atribuímos valores a x , conforme o número de horas que o cliente ficou no estacionamento e substituímos cada valor de x na função, por exemplo para x = 3 , que no caso representa 3 horas , temos 7 somado com 3(número de horas) multiplicado por 2( valor de cada hora ) . Totalizando 7 + 3 . 2 = 13 reais, valor que o cliente deve pagar. E assim fazemos com cada valor de x.
Observe que, a cada valor atribuído a letra x, obteremos um único valor para letra y. Exemplo:
- Para x = 9, temos:
y = 7 + 2x
y = 7 = 2. 0
y = 7 + 0
y = 7
Isso significa que, se o proprietário do carro não passar de 1 hora, pagará R$ 7,00
Dizemos que a grandeza y é função da grandeza x, se há entre elas uma correspondência. Vale dizer que: para cada valor de x, existe um único valor de y.
Também podemos dizer que y é uma função de x por y = f(x). Então, a função y = 7 + 2x pode ser representada por f(x) = 7 + 2x
RECAPITULANDO…
Vamos indicar por x o número de horas excedentes e por y o preço total a ser pago. Podemos, então, montar uma sentença com essas duas grandezas: y = 7 + 2x -> lei de formação
• para x = 1, temos:
y = 7 + 2.1
y = 7 + 2
y= 9
Se o motorista ficar 1 hora excedente, pagará R$ 9,00.
• para x = 2, temos:
y = 7 + 2.2
y = 7 + 4
y= 11
Se o motorista ficar 2 horas excedentes, pagará R$ 11,00.
Com isso, poderemos dizer que o preço (y) a pagar é obtido em função do número de horas extras (x) que o carro permanecer no estacionamento.
2ª SITUAÇÃO:
Em um parque de diversões, a entrada custa R$ 50,00 e cada brinquedo R$ 4,00. Leia o quadro e observe a relação entre a quantidade de brinquedos e o valor gasto:

EXPLICAÇÃO:
Ao entrar no parque de diversões a pessoa paga R$ 50,00, e a cada brinquedo que usa paga R$ 4,00, logo se utiliza por exemplo 3 brinquedos, pagará 50(reais) + 4 (preço de cada brinquedo) multiplicado por 3 (quantidade de brinquedos usados).

Agora, a partir da leitura atenta dessas informações, observe:
- Se uma criança brincar em 7 atrações, quanto gastará ao todo? Nesse caso, substituímos x por 7.
f(7) = 50 + 4.7
f(7) = 50 + 28
Logo, esta criança irá gastar R$ 78
- Se uma pessoa gastar com a entrada e os brinquedos R$ 90,00.
Em quantos brinquedos ela poderá andar?
Nesse caso, substituímos
f(x) por 90: f(x) = 90 —> 50 + 4x = 90
4x = 90 – 50
4x = 40
x = 40 / 4
x= 10
Essa pessoa poderá andar em 10 brinquedos.
REPRESENTAÇÃO DA FUNÇÃO ATRAVÉS DE DIAGRAMAS
Exemplo:
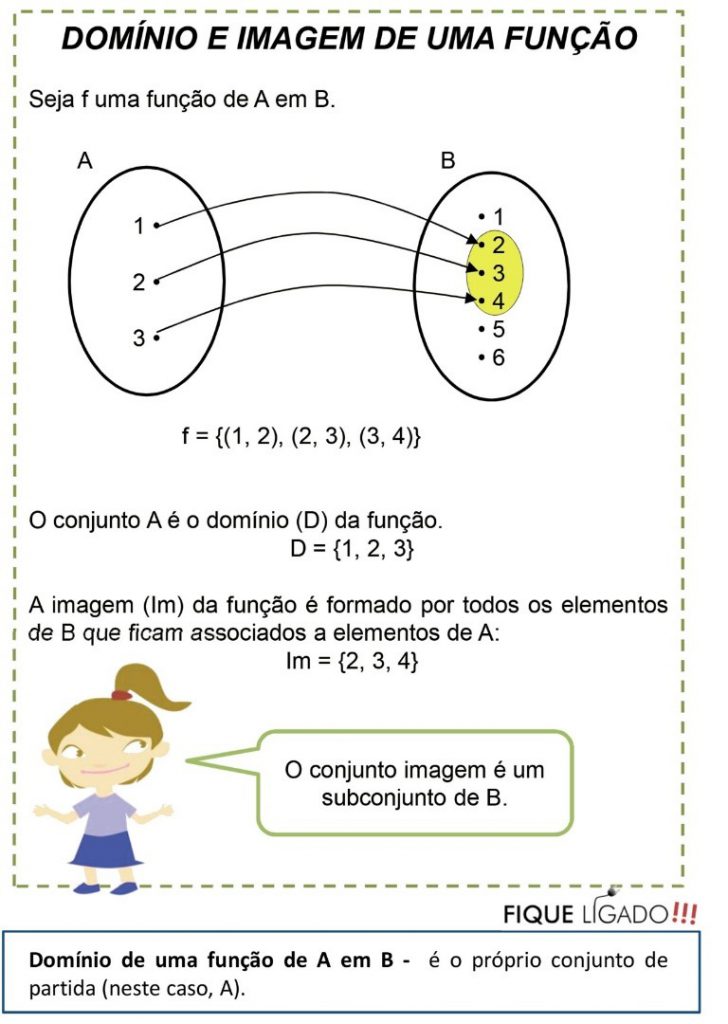
São funções de A em B, as relações representadas nos seguintes diagramas:
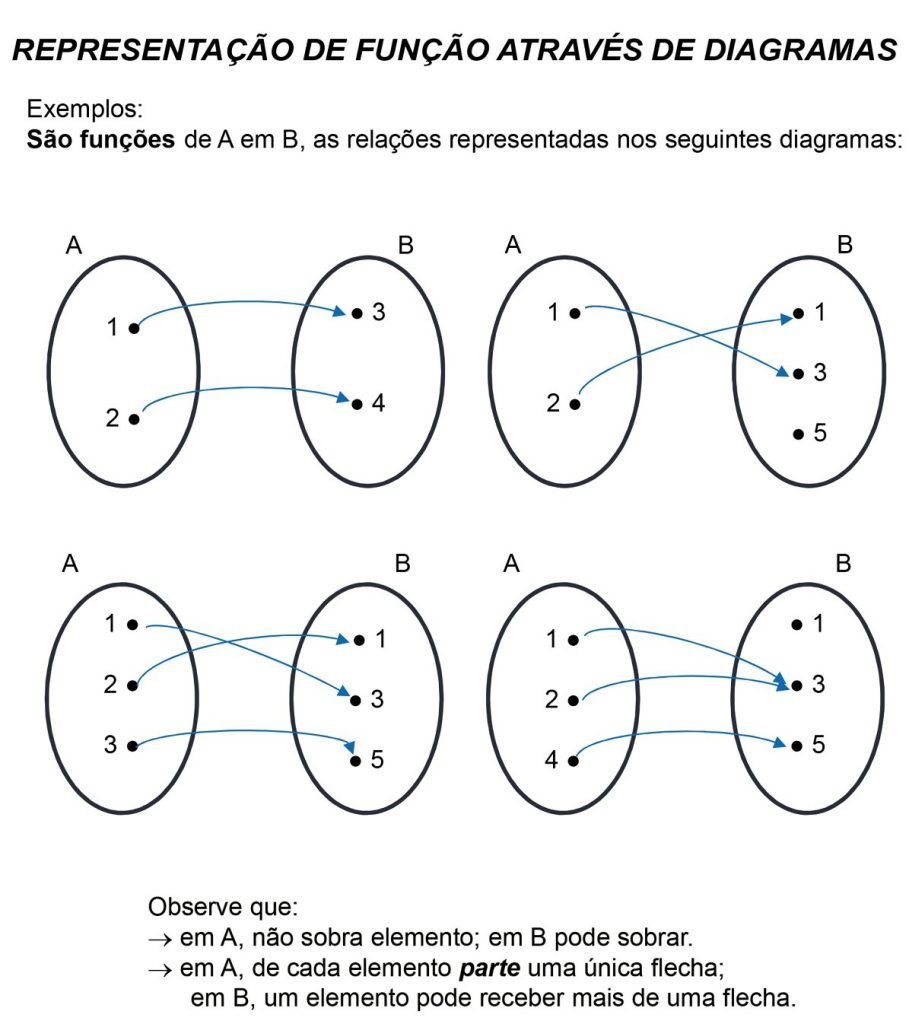
Observe que:
à Em A, não sobra elemento, em B pode sobrar.
- Em A, de cada elemento parte uma única flecha;
- Em B, um elemento pode receber mais de uma flecha.
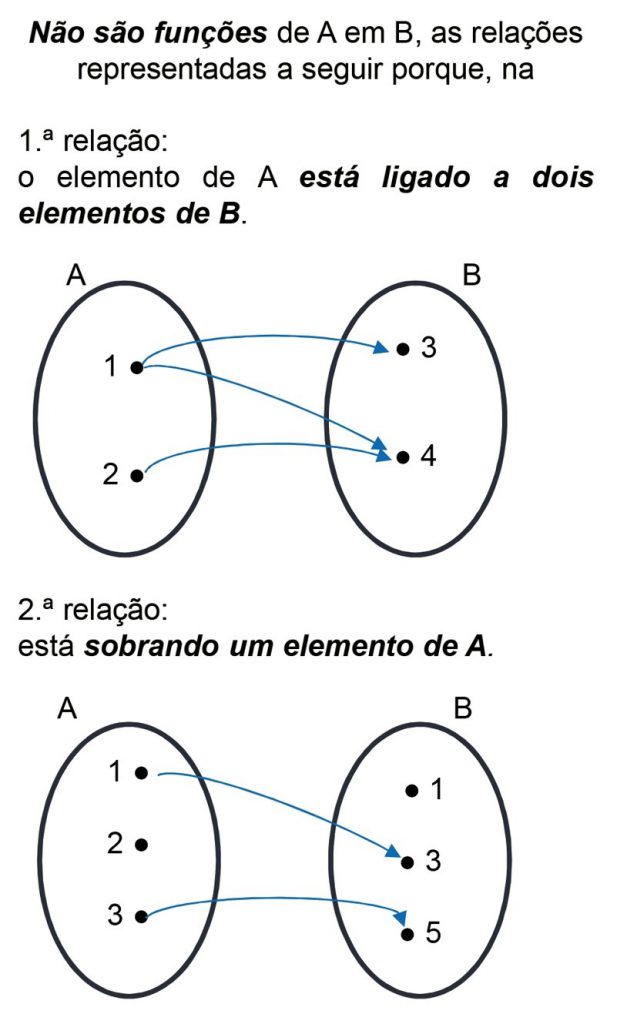
Não são funções de A em B, as relações representadas a seguir porque, na :
1ª RELAÇÃO: O elemento de A está ligado a dois elementos de B.
NOTAÇÃO DE FUNÇÃO
Considere a função f definida de IR em IR, tal que y = 2x – 1:
Para x = 2, teremos (y = 2x – 1) y = 2.2 -1 = 3
Para x = 3, teremos (y = 2x – 1) y = 2.3 – 1 = 5
Para x = 4, teremos (y = 2x – 1) y = 2.4 – 1 = 7
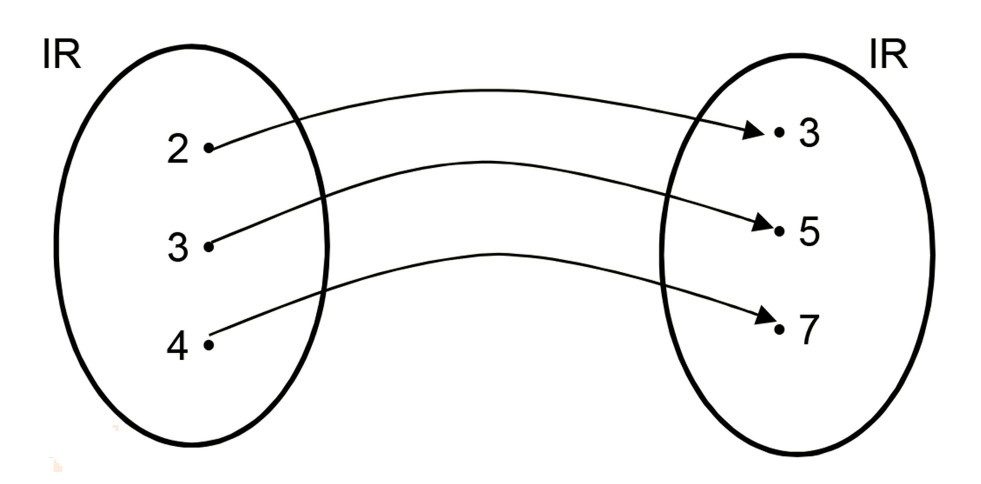
Dizemos que:
• 3 é a imagem de 2 pela função f. —> f(2) = 3
• 5 é a imagem de 3 pela função f. —> f(3) = 5
• 7 é a imagem de 4 pela função f. —> f(4) = 7
ATIVIDADE 2
Agora é com você. Observe o exemplo na letra “a” e faça a letra “b” das questões 1, 2 e 3.
Questão 1– Dada a função definida por f(x) = x + 2, calcule:
a) f (0)
Solução: Substituindo x por 0
f(0) = 0+2
f(0)= 0 + 2
f (0)= 2
b) f(-2)
Substituindo x por -2
f (-2) = (-2) + 2
f (-2) = ________
f (-2) = ________
Questão 2– Dada a função definida por f(x) = x2 – 3, calcule:
a) f (0)
Solução: Substituindo x por 0
f(0) = 0 – 3
f(0)= 0 – 3
f (0)= – 3
b) f(-2)
Substituindo x por -2
f(-2) = (-2)2 – 3
f(-2) = ________
f(-2) = ________
Questão 3– Dada a função definida por f(x) = 2x – 3, calcule:
- f(x) = 3
Solução: Igualando a função a 3
2x – 3 -3
2x = 3 + 3
2x = 6
x = 6/2
x = 3
b) f(x)=7 Chegamos ao final de mais uma aula sobre funções, aconselho que se você chegou ao final dessa aula e aparentemente não teve dúvida e conseguiu fazer as atividades, releia para ver se realmente entendeu, qualquer dúvida, o professor de Matemática é a quem você vai recorrer. Obrigado e até a próxima.
| Proponentes – Professores | Rubens Rodrigues Mendonça |
| Instituição Educacional | Escola Municipal Professora Marília Carneiro Azevedo Dias |
| CRE | CENTRAL |