Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento I (9º ano) do Ciclo da Adolescência foi veiculada na TV no dia 03/08/2021 (Quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.

Nesta atividade de matemática você estudará as relações métricas no triângulo retângulo e o Teorema de Pitágoras, ressaltando os seguintes conceitos: triângulo retângulo; relações métricas no triângulo retângulo e o Teorema de Pitágoras.
Assista a seguir, a videoaula do professor Bruno Silvestre com a temática: Relações métricas no triângulo retângulo e o Teorema de Pitágoras.
Como o professor Bruno disse na videoaula, para compreender o triângulo retângulo, as relações métricas no triângulo retângulo e o Teorema de Pitágoras é necessário compreender quais os principais elementos do triângulo retângulo. A imagem seguir apresenta algumas características dele, observe:
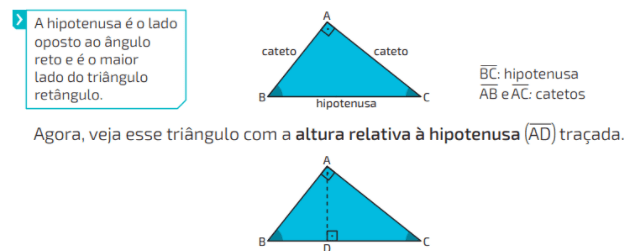
Ao traçar a altura, podemos destacar os triângulos retângulos ABC , ADC e ABD.
Veja como podemos verificar se esses triângulos são semelhantes entre si.
Inicialmente consideramos os três triângulos separadamente.
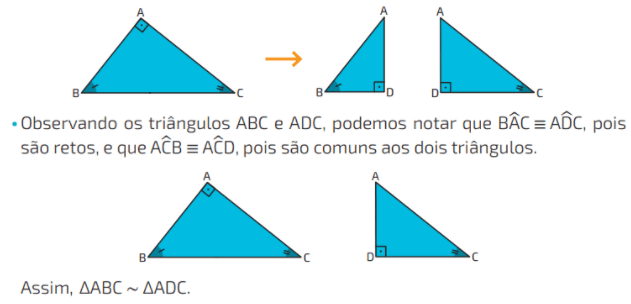
Como os triângulos ADC e ABD são semelhantes ao triângulo ABC, esses triângulos são semelhantes entre si, ou seja, ΔABC ∼ ΔADC ∼ ΔABD.
Em um triângulo retângulo a altura relativa à hipotenusa divide-o em dois outros triângulos retângulos, que são semelhantes ao maior e, consequentemente, semelhantes entre si.
A partir da semelhança desses triângulos, podemos estabelecer algumas relações entre as medidas do comprimento de seus lados. Para isso, indicaremos essas medidas com letras minúsculas.

Como em triângulos semelhantes os lados correspondentes são proporcionais, podemos escrever as seguintes proporções.
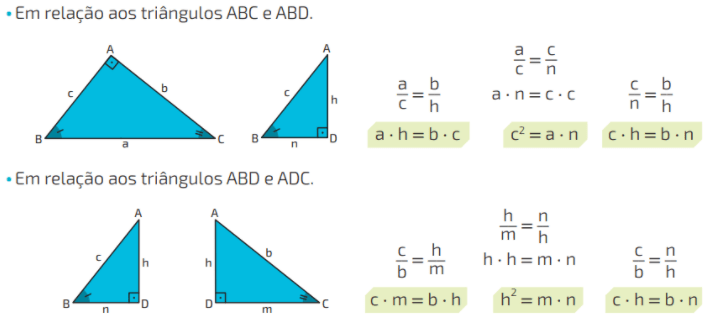

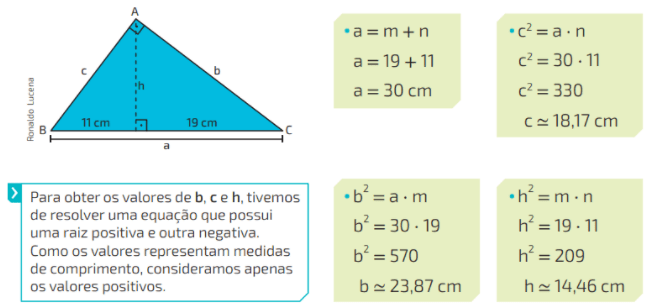
Utilizando as relações métricas, determinaremos os valores de a, b, c e h no triângulo retângulo a seguir.
Atividade 1
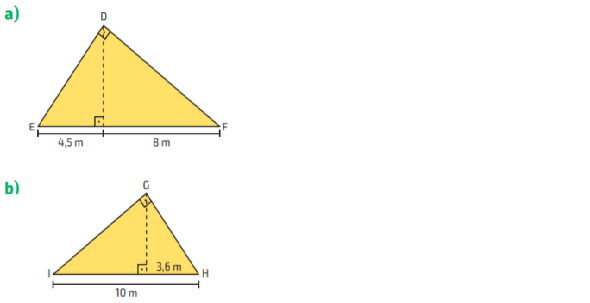
Agora que você já conhece todas as fórmulas para desenvolver as relações métricas no triângulo retângulo, calcule a medida do perímetro e a medida da área de cada um dos triângulos.
Chegamos ao ponto alto da atividade de hoje: o Teorema de Pitágoras.
Na videoaula acima, o professor Bruno nos contou um pouco da história do matemático e filósofo grego Pitágoras, que viveu por volta de 572 a.C. que desenvolveu o Teorema de Pitágoras, um importante conceito matemático. Esse teorema demonstra a relação entre os catetos e a hipotenusa do triângulo retângulo. Veja e explicação:

Podemos verificar essa relação por meio de figuras. Por exemplo, para um triângulo retângulo com lados medindo 3, 4 e 5 unidades de comprimento, consideramos três quadrados; cada um construído a partir de um lado do triângulo, conforme a figura ao lado.

Note que a medida da área do quadrado construído a partir da hipotenusa é igual à soma das medidas das áreas dos quadrados construídos a partir dos catetos, ou seja,
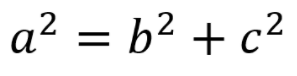
Observe o recurso manipulativo que o professor Bruno organizou para demonstrar a você, as relações existentes no Teorema de Pitágoras:

Atividade 2
Acesse o QR-Code ou o link https://drive.google.com/file/d/1Tm_d6INVcGhZ_WXmSzs0ixjTMyMOYOg-/view?usp=sharing para realizar uma atividade preparada pelo professor Bruno.

Acompanhe com atenção o exemplo resolvido abaixo, identificando o modo de utilizar corretamente o Teorema de Pitágoras, sucessivas vezes:
Para calcular a medida x :
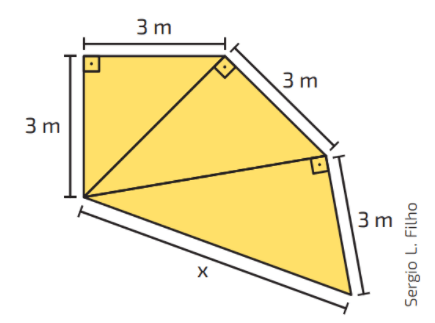
Para resolver e encontrar o valor de x, devemos primeiro encontrar por meio do Teorema de Pitágoras, as medidas das duas hipotenusas anteriores, para isso, vamos pensar na figura como sendo três triângulos retângulos distintos, chamando a primeira hipotenusa de a e a segunda hipotenusa de b, conforme mostra a imagem abaixo:
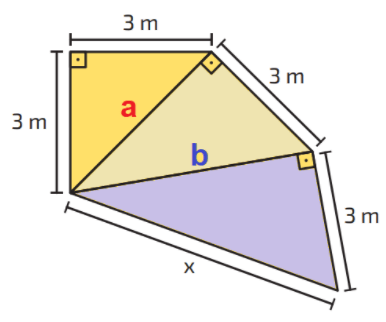


Atividade 3
Agora é com você! Resolva as questões a seguir envolvendo o conceito do Teorema de Pitágoras.
a) Pedro está construindo uma porteira com formato retangular para a entrada de sua fazenda. Ele precisa de uma ripa de madeira para fazer um reforço diagonal na estrutura retangular. De acordo com as medidas indicadas na imagem, qual deve ser a medida aproximada do comprimento dessa ripa?
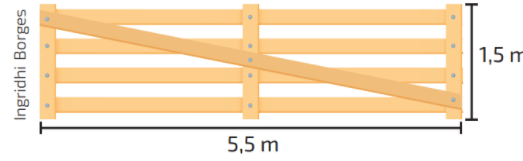
b) Uma viga de madeira com 6 m de comprimento foi apoiada em um muro como indicado a seguir.
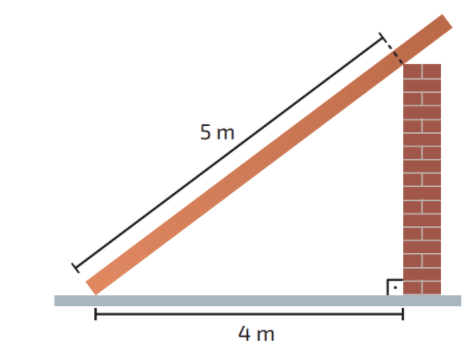
A que distância a base da viga deve ficar da base do muro para que o topo da viga coincida com o topo do muro?
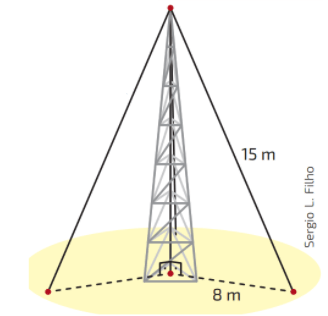
c) De acordo com a imagem ao lado, elabore um problema e depois procure resolver. Depois, verifique se você resolveu corretamente, utilizando o Teorema de Pitágoras.
RELEMBRANDO!
Nesta atividade você estudou sobre as relações métricas no triângulo retângulo, percebendo que elas se originam da divisão de um triângulo retângulo em três triângulos semelhantes por meio do traçado da altura relativa à hipotenusa do triângulo maior, em seguida deu continuidade aos estudos do triângulo retângulo por meio do Teorema de Pitágoras, conhecendo um pouco da história deste homem fenomenal para a cultura humana, sobretudo matemática, percebendo algumas de suas demonstrações e situações problemas que envolvam o conceito do Teorema de Pitágoras.
Parabéns, continue com empenho em seus estudos matemáticos. Até a próxima atividade!
| Referências | IEZZI, Gelson., MACHADO, Antônio., DOLCE, Osvaldo. Matemática e realidade 9º ano – 9. ed. – São Paulo : Atual Editora, 2018. PATARO, Patrícia Moreno., BALESTRI, Rodrigo. Matemática essencial 9o ano : ensino fundamental, anos finais – 1. ed. – São Paulo : Scipione, 2018. PNLD |
| Componente Curricular | Habilidade |
| Matemática | Habilidades Estruturantes (EF09MA10) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal. (EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos. (EF09MA14-B) Ler, interpretar, resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade, envolvendo retas paralelas cortadas por secantes. Habilidades Complementares EF09MA14-A |
