Olá, educando (a)! Esta videoaula de Matemática para o 8º ano do Ensino Fundamental – foi veiculada na tv no dia 31/03/2021 (quarta-feira). Aqui no portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 8º ano, irá estudar sobre as potências de números inteiros, compreendendo-a como a operação inversa do processo de radiciação.

Assista a videoaula abaixo, com a temática: Potenciação e Racionalização
Olá, nesta atividade você irá perceber o que são potências e quais as suas possíveis relações com a radiciação, compreendendo que uma é a operação inversa da outra. Para iniciar seus estudos, leia com atenção sobre as potências dos números naturais.
Potenciação com números naturais
A operação de potências em matemática nada mais é do que a multiplicação de fatores iguais. Em potência tem-se dois elementos principais: uma base e um expoente.
Observe:
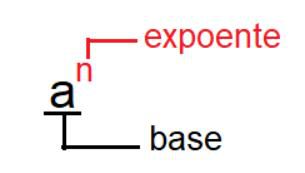
A base indica o número que deverá ser multiplicado por ele mesmo e o expoente a quantidade de vezes que o número deverá ser multiplicado por ele mesmo.
Para compreender melhor, veja a explicação abaixo:

Assim, a operação em que se tem uma base e um expoente indica uma multiplicação de fatores iguais denominada potenciação.
Veja alguns exemplos e resolução das potências:
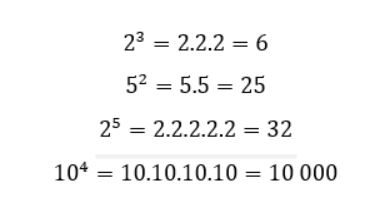
Há algumas regras que envolvem as potências com números naturais, veja:
As potências que tem como expoente um (1) geram o próprio número, pois não exige que seja feita nenhuma multiplicação;
Já as potências que possuem expoente zero (0) são sempre iguais a um;
Exemplos:
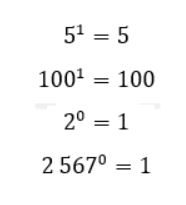
As potências por sua vez, podem indicar uma padronização entre sequências de figuras geométricas.
Observe com atenção!
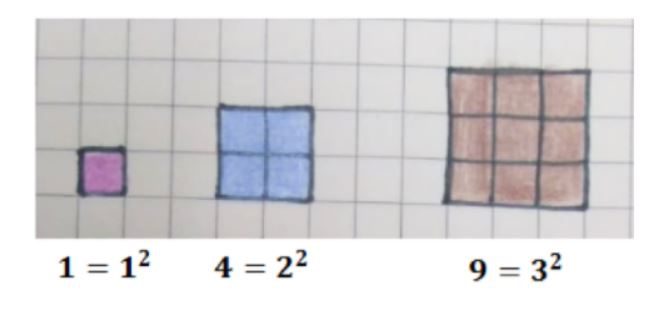
A imagem extraída do livro “Pedro Potenciano”, indicam uma sequência de figuras que se inicia com um quadradinho, depois com quatro quadradinhos, seguido de nove quadradinhos e assim sucessivamente. Se você observar com muita atenção, verá que a quantidade de quadradinhos na base de cada figura ao quadrado (elevado a dois), ou seja, colocando o expoente dois (2), gera a quantidade de quadradinhos da figura. Assim, você seria capaz de falar qual seria a próxima figura e dizer quantos quadradinhos ela terá?
Após pensar um pouco, fica evidente que a próxima figura ter o total de 16 quadradinhos, pois na base ela terá 4 quadradinhos, logo:
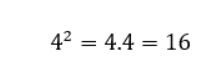
Uma outra sequência geométrica que faz uso das potências é a ilustrada abaixo, também, disponível no livro “Pedro Potenciano”.
Observe com atenção:
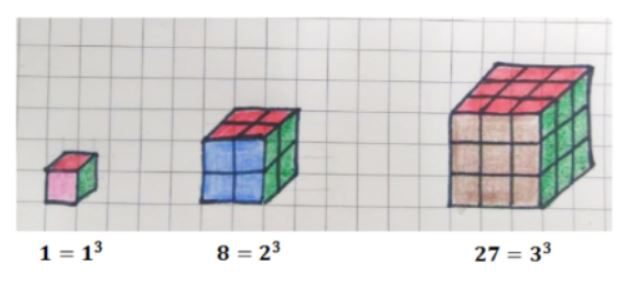
Nesta sequência, como as figuras representam algo tridimensional, na forma de cubinhos menores que formam um cubo maior composto pelos menores, é fácil perceber que, a quantidade de cubos da base de uma das faces ao cubo (expoente 3) resulta na quantidade de cubinhos totais de cada figura. Nesta linha de raciocínio, você seria capaz de identificar quantos cubinhos comporiam a próxima figura dessa sequência?
Assim como na outra sequência geométrica, na base de cada face apareceriam 4 cubinhos, então é só fazer a potenciação do quatro como base e o três como expoente:
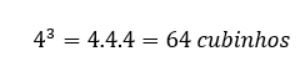
Com esses dois exemplos, nota-se que:
Quando se tem uma figura plana em forma de quadrado, pode-se aplicar a potenciação com expoente 2, ou, comumente conhecido como elevar o número ao quadrado. A palavra quadrado aqui expressa a figura, amplamente conhecida por vocês como quadrado.
Quando se tem uma figura representada em sua forma tridimensional, utiliza-se o expoente 3, ou, popularmente conhecido como cubo (elevar a base ao cubo), pois indicam a representação cúbica das figuras.
Viu como é fácil determinar o resultado de uma potenciação com números naturais? Agora que você já está expert em potenciação com números naturais, vamos ampliar esse conceito para os números inteiros.
Potenciação com números inteiros
A potenciação com números inteiros segue a mesma lógica com os números naturais, só que agora, tanto a base quanto o expoente podem ser números negativos.
Para iniciar seus estudos, com as bases que podem ser negativas ou positivas, considerando por enquanto somente expoentes positivos.
Para isso observe os exemplos:
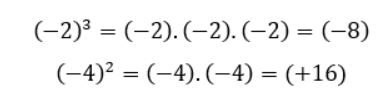
As duas situações nos mostram que, quando se tem a base negativa, deve-se proceder multiplicando os sinais e também os números (vale ressaltar, aqui, as operações com sinais amplamente estudadas no sétimo ano). Além disso, pode-se indicar duas situações relevantes:
- Uma potência com base negativa e expoente ímpar, resultará sempre em um número negativo;
- Uma potência com base negativa e expoente par, resultará sempre em um número positivo.
Assim, potências com expoentes, absurdamente grandes podem ser facilmente respondidas, conforme mostra o exemplo:
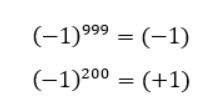
E quando, se tem um expoente negativo? Como resolver a potência?
Para determinar uma potência com expoente negativo, basta transformar o expoente negativo em um expoente positivo, para isso, deve-se inverter a base, em seguida, resolve-se normalmente a potência.
Exemplo:
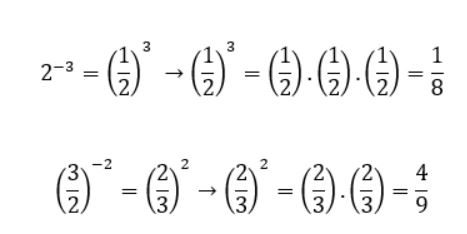
Note que o expoente negativo, geralmente produz uma fração, e, esta fração por sua vez, torna-se a base da potência. Assim, você deve resolver a potenciação com a multiplicação das frações.
Estudo das raízes quadradas e cúbicas
Agora que você sabe tudo sobre as potenciações, vamos dar início ao estudo das raízes quadradas e cúbicas.
O conceito de radiciação em matemática é muito semelhante ao de potenciação, pois uma operação é o inverso da outra. Mas antes de desenvolver essa propriedade de inversos, conheça os elementos que constituem a radiciação:
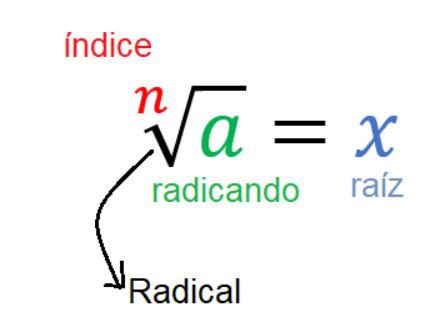
Assim, a radiciação possui quatro elementos principais: o símbolo radical, o índice da raíz, o radicando (o qual se deseja extrair a raíz) e a resposta da radiciação que é a raíz.
Como já mencionado, a radiciação é o inverso da potenciação, veja o seu conceito algébrico:
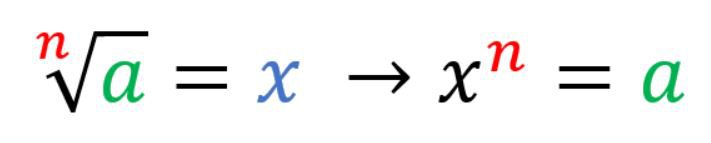
Agora observe esse comportamento com números:
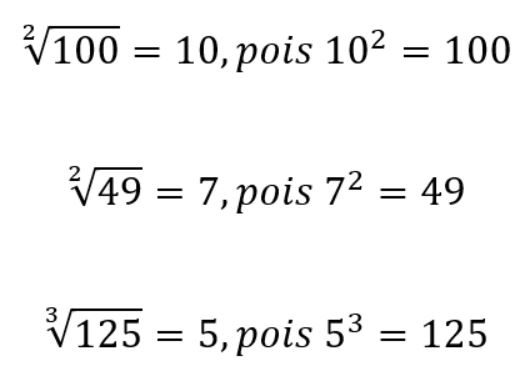
Números quadrados perfeitos
Para compreender melhor sobre as raízes quadradas (que tem índice 2), analise a situação abaixo:


Os números quadrados perfeitos, são números que possuem raíz quadrada, ou seja, são os números que podem se escritos na forma de uma multiplicação de um número por ele mesmo.
Agora é com você!
Leia atentamente as instruções abaixo e determine o que se pede:
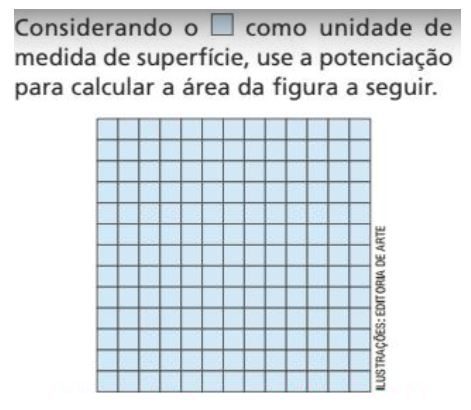
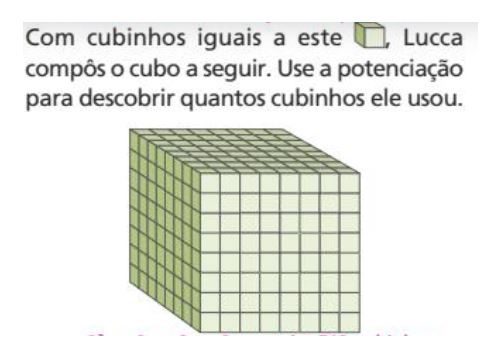
Analise a situação problema abaixo e responda o que se pede:
Resolva as raízes quadradas e cúbicas:

Marque um x no único número que não é um quadrado perfeito.

Em síntese, nesta atividade você teve a possibilidade de estudar sobre as potenciações e radiciações, verificando os procedimentos necessários para a resolução desses conceitos tão importantes na matemática. Além de desenvolver estudos sobre as potências e as raízes, você também teve a oportunidade de desenvolver situações problemas, colocando em prática os estudos desenvolvidos nesta aula.
Te esperamos até a próxima atividade de matemática.
Até lá. Bons estudos!
| Referências – Texto elaborado com fins pedagógicos. | SILVESTRE, B. S. Pedro Potenciano: o garoto que investigou sobre as potências. Ed. Cia do Ebook. Timburi – SP, 2019. |
| Habilidades | Habilidades Estruturantes (EF08MA01-B) Efetuar, em contextos significativos, cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica. (EF08MA02-A) Reconhecer a importância da potenciação e da radiciação na resolução de problemas, fazendo uso de suas propriedades operatórias, incluindo a racionalização de denominadores, além de compreendê-las como operações inversas. Habilidades complementares EF08MA02-B EF08MA02-C |
Professor, essa aula segue a Matriz Curricular das Habilidades Estruturantes 2021-2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido à pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 147/2020 Dirped).
