Olá, educando (a)! Esta videoaula de Matemática para o 7º ano do Ensino Fundamental – foi veiculada na tv no dia 30/03/2021 (terça-feira). Aqui no portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 7º ano, terá a oportunidade de estudar sobre o cálculo de porcentagens na vida cotidiana e nas relações sociais humanas de comércio, compreendendo uma parte da matemática financeira.
Bons estudos!

Assista a videoaula abaixo, com a temática: Porcentagens de um número natural
BRUNO SILVA SILVESTRE
Olá, nesta atividade você vai aprender sobre alguns conceitos de porcentagem e matemática financeira. Você já ouviu falar sobre porcentagens?
Com certeza, você já deve ter ouvido ou visto algo envolvendo porcentagens, mas você sabe o que são porcentagens?
Na imagem abaixo, tem-se algumas situações onde utiliza-se a porcentagem, observe atentamente:

Nos exemplos observa-se que as porcentagens podem se referir às transações comerciais e de produção de determinado produto, mas não se limitam a essas duas situações.
Calculando porcentagens por meio da proporção
A porcentagem é um conceito matemático que toma como referência a centena, tendo como foco o seu parâmetro. Para entender melhor, observe os exemplos:
Exemplo 01. Thiago quer comprar uma bicicleta que custa R $300,00. Essa bicicleta está com desconto de 15%. Qual o valor a ser pago por Thiago na bicicleta, após aplicado o desconto?

Para resolver a situação podemos pensar na seguinte proposta:
15% de alguma coisa, representa que, a cada 100 itens, tem-se a referência de 15, ou seja:
15% de 100, significa que a cada 100 itens toma-se 15.
No caso da bicicleta que envolve dinheiro:
15% de R$ 100 = R$ 15 reais
Logo, se dobrarmos o valor de 100 para 200, temos a aplicação dos R$ 15 duas vezes, que dá R$ 30,
15% de R$ 200 = R$ 30
E fazendo para R$ 300, tem-se:
15% de R$ 300 = R$ 45, logo nossa organização de proporcionalidade, fica assim:

Assim, descobrimos que o valor de DESCONTO de 15% de R $300 é igual a R $45.
Assim o valor da bicicleta como desconto de 15% pode ser dado pela subtração:
300 – 45 = 255
O valor da bicicleta aplicado o desconto é de R $255.
Com o exemplo, pode-se pensar em qualquer situação problema resolvida por meio da proporcionalidade. Atente-se à nova situação problema:
Exemplo 02. Rosa foi comprar um carro à vista (quando se tem a intenção de não parcelar e fazer o pagamento em uma única vez). O valor do carro era de R $50.000, porém, à vista, havia um desconto de 8%. Qual foi o valor de desconto obtido por Rosa, na compra do carro à vista?

Vamos proceder conforme exemplo da situação anterior:

Logo, o valor do desconto obtido por Rosa é de: R $4 000.
Com esses dois exemplos percebe-se que as porcentagens facilmente podem ser calculadas utilizando a proporção! Uma outra forma de calcular as porcentagens é por meio da fração de quantidade ou regra de três simples.
Calculando porcentagens por meio das frações de quantidade
As porcentagens, podem ser facilmente transformadas em frações ou números decimais.
Como as porcentagens representam algo que tem parâmetros de 100, basta escrever a porcentagem em uma fração que tenha denominador 100, e, se quizer transformar a fração em número decimal, o mesmo pode ser realizado conforme a tabela:
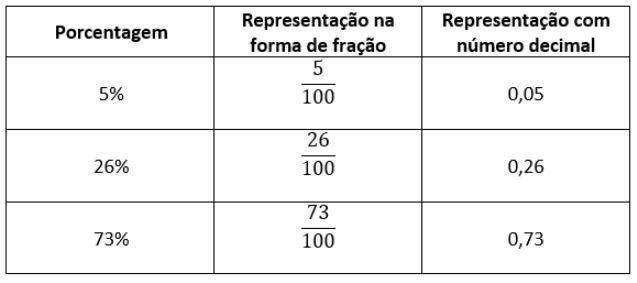
Com essas transformações, é possível que se realize, também, cálculos de porcentagens.
Exemplo 03. Calcule 12% de R$ 200.
Para resolver a situação, basta transformar 12% em fração e calcular a sua fração de quantidade:

Nota-se que as porcentagens estão presentes em nossas relações comerciais e representam uma parte do todo, em que tem-se a referência por 100, por isso se chama porcentagem!
A imagem abaixo expressa algumas porcentagens e sua representação em tamanho do todo. Observe:
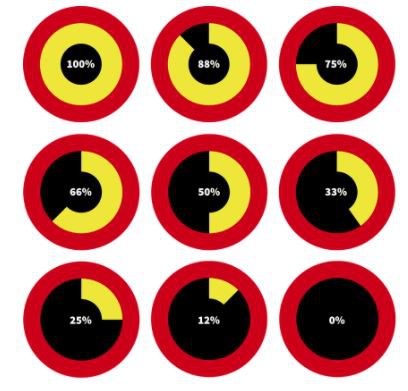
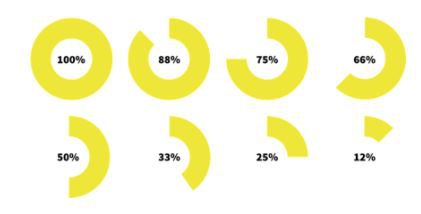
Na imagem é possível perceber que quanto mais a porcentagem se aproxima de 100% maior é a sua representação do todo e quanto menor, menos se representa o todo.
Agora é com você! Resolva as situações problemas abaixo:
Questão 01. Sr. Raimundo tem 4 netas: Ana, Júlia, Maria e REnata, e, pretende dividir o valor de R$ 10 000 entre elas, sabendo que Ana receberá 45%, Júlia receberá 25%, Maria Eduarda 20% e Renata 10% dessa quantia, responda:
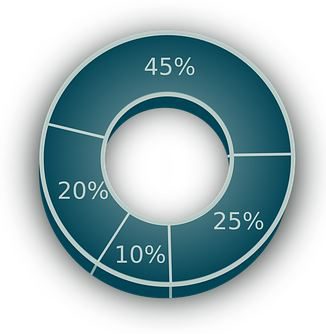
Sem fazer nenhum cálculo escrito, somente utilizando-se do cálculo mental, qual neta receberá o maior valor? Qual neta receberá o menor valor?
Questão 02. Agora, realizando os cálculos que achar mais conveniente, considere todos os dados da questão anterior e responda quantos reais a neta Ana irá receber?
Questão 03. Sr. Raimundo deseja comprar um carro que custa R$ 30 000. Se o carro está com desconto de 5%, qual será o valor pago por Sr. Raimundo no carro, utilizando-se já do desconto?
Questão 04. Se 10% de uma determinada quantia é R$ 50, determine o valor total dessa quantia.
Em síntese, nesta atividade você observou e estudou algumas situações envolvendo as porcentagens, realizando exercícios por meio de situações problemas que contextualizam os estudos de forma prática. Continue acessando o portal Conexão Escola e amplie os seus estudos. Até a próxima atividade de Matemática.
Aguardamos você na próxima atividade, até lá!
Bons estudos!
| Habilidades | Habilidades Estruturantes (EF06MA13-B) Ler, interpretar, resolver e elaborar problemas que envolvam porcentagens, com base na ideia de proporcionalidade, sem fazer uso da regra de três, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros. (EF07MA02-B) Ler, interpretar, resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros. Habilidade Complementare EF06MA06-C |
Professor, essa aula segue a Matriz Curricular das Habilidades Estruturantes 2021-2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido à pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 147/2020 Dirped).

