Olá, educando (a)! Esta videoaula de Matemática para a 7ª série da Eaja – foi veiculada na TV no dia 18/03/2021 (quinta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade você irá aprender um pouco mais sobre a potenciação e a radiciação, vai perceber que são operações inversas e bastante usadas no cotidiano das pessoas.

Quel tal? Vamos aprender um pouco mais sobre esse assunto pra lá de interessante?
Então pegue seu material e preste bastante atenção às explicações do professor Hélio Roberto da Rocha.
Hoje você irá aprender um pouco mais sobre as potenciações e radiciações.
Antes de começar, quero mostrar a você alguns assuntos que se utilizam dessas duas operações.
Você vai perceber que é necessário ter esse conhecimento.
Em vários momentos de nossas vidas nos deparamos com cálculos que envolvem essas duas operações, as mais utilizadas são:
Nos cálculos de juros
Nas notações científicas utilizadas para escrever os números com menos caracteres, por exemplo:
a velocidade da luz é aproximadamente:
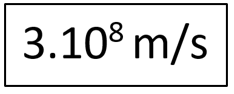
a distância entre o sol e a Terra, 150 milhões de quilômetros que pode ser escrito na forma

Para informar a quantidade de memória de smartphones, por exemplo, 8Gb de memória RAM que equivale a
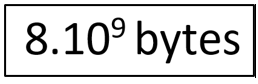
Alguns exemplos onde se utiliza a Radiciação
Caso você necessite calcular quantas polegadas tem sua TV, utiliza-se a seguinte fórmula:
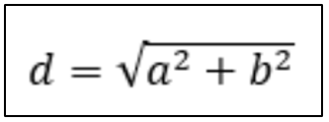
Onde a e b são as medidas da largura e do comprimento da TV (lembrando que 1 polegada é aproximadamente 2,6cm)
Existe uma fórmula na Física que calcula a velocidade, aproximada de um do carro, dado o comprimento (d) da marca do pneu no asfalto, veja:
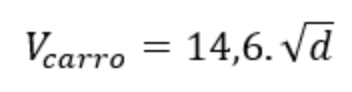
Viu o tanto que é importante saber um pouco sobre Potenciação e Radiciação.
Antes de propor alguns problemas a você, é necessário informar algumas definições sobre o assunto.
Potenciação (Definição): é uma operação matemática utilizada para escrever um número que está sendo multiplicado várias vezes, ou seja, é uma multiplicação de fatores iguais.
Exemplo1:
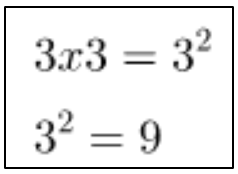
Onde: 3 é denominado de base, 2 de expoente e o resultado, 9, é denominado de potência.
Radiciação (Definição): é a operação inversa da potenciação, ou seja, enquanto a potenciação determina o resultado de uma multiplicação de fatores iguais, a radiciação procura determinar esses fatores.
Exemplo2:
Qual seria a raiz quadrada de 9?

O número 9 chamamos de radicando e o 3 de raiz quadrada.
Percebeu que a potenciação é o inverso da radiciação.
Exemplo 3:
Qual é a raiz cúbica de 27?
E agora como escrever raiz cúbica? Basta acrescentar um 3 no radical. Veja:

Para representar a raiz quarta só colocar o 4 no lugar do 3. Então respondendo o exemplo

Tivemos que determinar um número para multiplicá-lo três vezes para encontrar 27.
Se você compreendeu, faça no seu caderno a raiz quarta de 64.
Antes de passar para alguns problemas de aplicação, temos que estudar um pouco sobre as propriedades e operações da potenciação e radiciação.
Para esta atividade não ficar muito extensa, preparei alguns vídeos para você.
Vamos comigo!!
Após estudar toda a atividade e assistir aos vídeos, quero que você copie e resolva no seu caderno os problemas abaixo que preparei para você.
Problema 1 (Exemplo de potenciação)
Suponha que você é um mestre em obras, e precisa comprar o piso para assentar uma sala. A sala tem a forma de um quadrado de lado igual a 7m. Se o metro quadrado de piso custa R$98,00, quantos reais o proprietário da construção irá gastar?
Você já estudou que a área de um quadrado é dada por Área = lado x lado. Representando a medida do lado com a letra l e a medida da área por A, essa fórmula pode ser escrita assim:
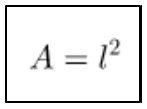
Observe que nesta fórmula, temos uma potenciação.
Substituindo a medida do lado por 6, obtemos A=7×7=49, logo a área é igual a 49 metros quadrados, uma ótima sala por sinal. Agora o valor que o proprietário irá gastar será de 49 x 98 = 4802 reais.
Problema 2 (Exemplo de radiciação)
Agora, você precisa passar uma fiação de um ponto da sala a outro no sentido da sua diagonal. Quantos metros de fio serão necessários para isso? Neste caso, usemos a fórmula da diagonal do quadrado. Veja a figura.
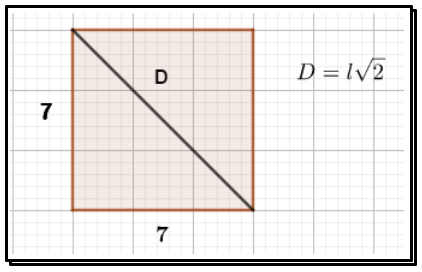
Substituindo a medida do lado por 7 e aproximando o valor da raiz quadrada de 2 por 1,4, obtemos D=7×1,4=9,8. Portanto o comprimento do fio deve ser aproximadamente 10 metros.
Para finalizar vamos ao último problema desta atividade, o título dessa atividade.
Problema 3
Suponha que você teve que frear bruscamente seu carro pois um cachorrinho entrou na sua frente na Av. Mutirão, logo apareceu um policial de trânsito para avaliar o ocorrido. Você disse a ele que estava na velocidade permitida. O policial pegou uma trena e mediu o comprimento das marcas do pneu deixada no asfalto. O valor dessa medida foi de 49m e a velocidade permitida naquela via é de 60km/h. Precisamos saber se a sua velocidade estava permitida.
E agora, como será que o policial calculou a velocidade. Simples, ele usou uma fórmula elaborada pelos cientistas.
A velocidade, aproximada, do carro dada de acordo com a medida do comprimento das marcas do pneu no asfalto é dada por:
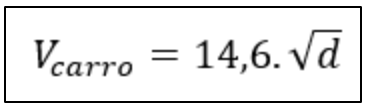
Substituindo o valor de d por 49, extraindo sua raiz quadrada, que é igual a 7, e em seguida multiplicamos por 14,6 e obtemos uma velocidade de aproximadamente 102 km/h.
E aí você estava dentro do permitido? Acho que não.
Bom, terminamos esta atividade!
Espero que você tenha gostado!
Abraços e até a próxima!
| Objetivos de Aprendizagem e Desenvolvimento | Potenciação e radiciação: – Potenciação e suas propriedades Potência com expoente fracionário – Radiciação Potenciação – Radiciação como operações inversas (EAJAMA0703) Reconhecer a importância da potenciação e da radiciação na resolução de situações-problema, fazendo uso de suas propriedades operatórias, além de compreendê-las como operações inversas. (EAJAMA0704) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).
