Olá, educando (a)! Esta videoaula de Matemática para a 4ª série da Eaja – foi veiculada na TV no dia 09/03/2021 (terça-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta aula falaremos de igualdade, equivalência e sobre a relação de igualdade entre dois membros, explorando suas propriedades na adição e subtração.
IGUAL?
DIFERENTE?
EQUIVALENTE?
QUER SABER? ENTÃO, ASSISTA A VIDEOAULA A SEGUIR, COM A TEMÁTICA: RELAÇÃO DE IGUALDADE EM ENTRE DOIS MEMBROS
VAMOS NESSA?!
OLÁ, OLÁ, ESPERO QUE ESTEJA TUDO BEM COM VOCÊ E SUA FAMÍLIA! ESTAMOS AQUI HOJE PARA UMA AULA BEM LEGAL.
VAMOS ESTUDAR HOJE SOBRE A RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS. VOCÊ VAI VER QUE É BEM TRANQUILO ESSE TEMA!
VOCÊ JÁ PAROU PARA PENSAR SOBRE O QUE É IGUALDADE?
NA IMAGEM A SEGUIR TEMOS ALGUNS PARES DE DESENHOS QUE PARECEM SER IGUAIS…
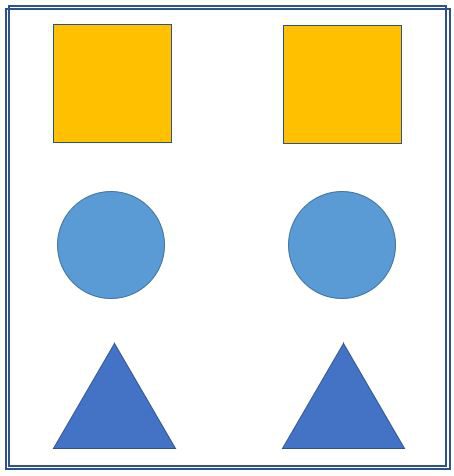
TEMOS AÍ 3 PARES DE IMAGENS FACILMENTE IDENTIFICADAS POR IGUAIS. SÃO ELAS:
- 2 CÍRCULOS,
- 2 QUADRADOS
- 2 TRIÂNGULOS EQUILÁTEROS
VEJAMOS AGORA A SEGUNDA IMAGEM:
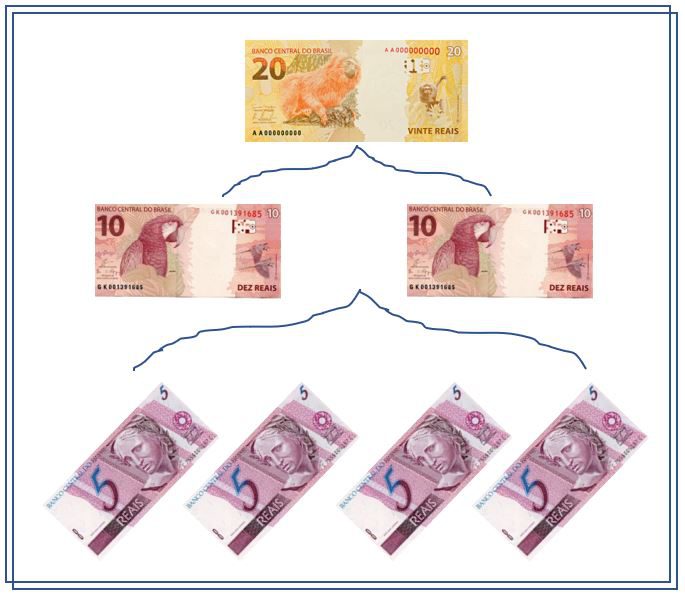
VEJA QUE TEMOS:
- 1 PAR DE CÉDULAS DE DEZ REAIS
- 4 CÉDULAS DE CINCO REAIS
- UMA CÉDULA DE VINTE REAIS
NATURALMENTE AS CÉDULAS DE DEZ SÃO IGUAIS E AS DE CINCO TAMBÉM SÃO IGUAIS ENTRE SI, MAS OS 3 TIPOS DE NOTAS APRESENTADAS SÃO DIFERENTES ENTRE SI, OU SEJA, A DE R$ 20,00 É DIFERENTE DA DE R$ 10,00, QUE SÃO DIFERENTES DAS DE R$ 5,00.
E O QUE QUEREMOS ENTÃO? DEMONSTRAR QUE EMBORA AS NOTAS SEJAM DIFERENTES, ESTAS NOTAS NAS QUANTIDADES APRESENTADAS SÃO EQUIVALENTES, OU SEJA, EMBORA SEJAM DIFERENTES, DUAS NOTAS DE R$ 10,00 EQUIVALEM A UMA DE R$ 20,00 E 4 NOTAS DE R$ 5,00 TAMBÉM EQUIVALEM A NOTA DE R$ 20,00.
VAMOS APROFUNDAR UM POUQUINHO MAIS SOBRE O TEMA DA AULA DE HOJE:
RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS.

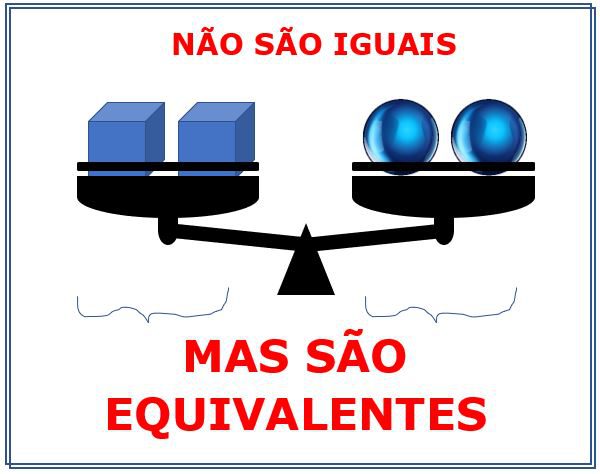
VEJA ESTA BALANÇA:
NO PRIMEIRO PRATO DOIS CUBOS E NO SEGUNDO, DUAS ESFERAS.
SÃO PEÇAS DIFERENTES, MAS OBSERVE QUE A BALANÇA ESTÁ EQUILIBRADA, OU SEJA, AMBOS OS PRATOS POSSUEM O MESMO VALOR EM MASSA, O PESO É IGUAL, MAS AS PEÇAS SÃO DIFERENTES.
ENTÃO DIZEMOS QUE HÁ AQUI UMA EQUIVALÊNCIA, O PESO DOS CUBOS É IGUAL AO PESO DAS ESFERAS.
VAMOS AOS NÚMEROS ENTÃO!
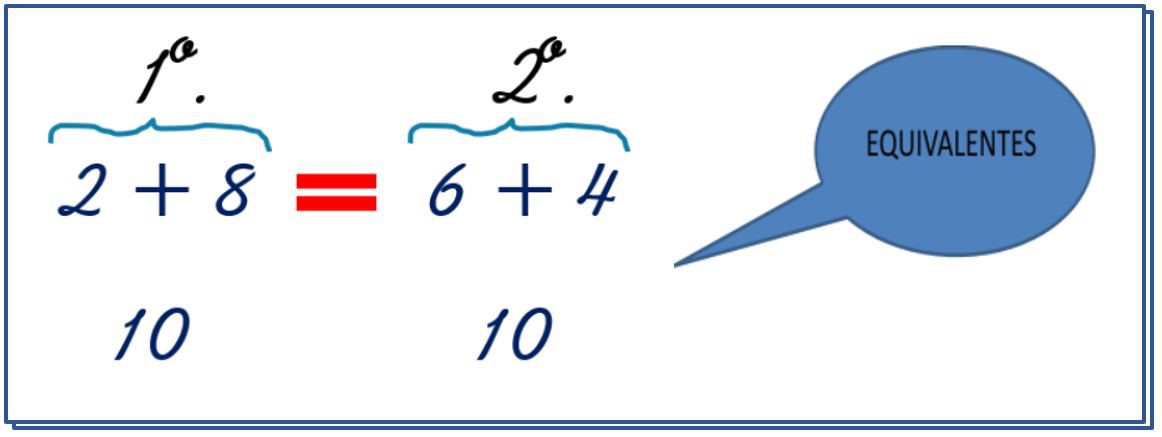
VAMOS COMEÇAR PELA OPERAÇÃO DE ADIÇÃO. VAMOS VER AQUI 2 + 8 = 10, PORQUE SÃO DUAS UNIDADES MAIS 8 UNIDADES E A SOMA É IGUAL A 10. QUE OUTROS NÚMEROS POSSO SOMAR QUE TAMBÉM VÃO TER RESULTADO IGUAL A 10. EU PENSO AQUI AGORA EM 6 + 4 = 10, OU SEJA, SEIS UNIDADES MAIS QUADRO UNIDADE É IGUAL A DEZ OU UMA DEZENA.
VEJA QUE AS DUAS OPERAÇÕES, AQUI NA ESQUERDA EU TENHO O PRIMEIRO MEMBRO E NA DIREITA O SEGUNDO MEMBRO, CHEGAM AO MESMO RESULTADO, MESMO COM NÚMEROS DIFERENTES, OU SEJA ESTAS OPERAÇÕES SÃO EQUIVALENTES, E A ISSO CHAMADOS DE RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS.

VEJA OUTRO EXEMPLO:
5 + 3 = 8
QUE OUTROS NÚMEROS PODEMOS USAR PARA TER UM RESULTADO IGUAL A 8?
PODE SER:
7 +1 = 8
ENTÃO 7 +1 = 8, OU SEJA, SÃO OPERAÇÕES EQUIVALENTES, POSSUEM UMA RELAÇÃO DE IGUALMENTE ENTRE SEUS MEMBROS.
SE VOCÊ PENSOU EM OUTROS NÚMEROS, PODE ESTAR CERTO TAMBÉM PORQUE HÁ OUTRAS POSSIBILIDADES.
DO MESMO MODO QUE FIZEMOS NA ADIÇÃO, VAMOS RELEMBRAR AQUI NA OPERAÇÃO DE SUBTRAÇÃO.
POR EXEMPLO:
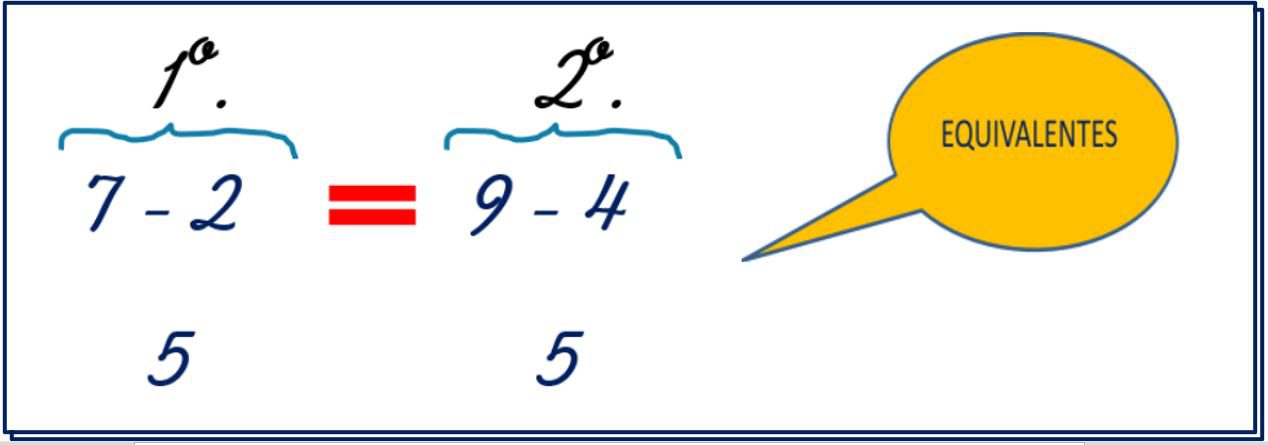
7 – 2 = 5
7 UNIDADES MENOS DUAS UNIDADES, O RESULTADO É CINCO.
QUE OUTROS NÚMEROS POSSO USAR QUE SUBTRAÍDOS TENHO RESULTADO IGUAL A 5?
POR EXEMPLO:
9 – 4 = 5
DA MESMA MANEIRA, VOCÊ PODE PENSAR EM OUTROS NÚMEROS QUE TAMBÉM VAI DAR SUPER CERTO.
AQUI À ESQUERDA, TEMOS O PRIMEIRO MEMBRO E À DIREITA O SEGUNDO MEMBRO. AMBOS OS MEMBROS SÃO EQUIVALENTES PORQUE POSSUEM O MESMO RESULTADO, INDEPENDENTE DOS NÚMEROS USADOS NA SUBTRAÇÃO, DEMONSTRANDO UMA RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS.

VEJA OUTROS EXEMPLOS DESSA RELAÇÃO:
10 – 3 = 7
8 -1= 7
VOCÊ PODE PENSAR NOVAMENTE EM OUTROS NÚMEROS POIS SÃO MUITAS AS POSSIBILIDADES.
POR EXEMPLO:
9 – 2 = 7
11 – 4 = 7
14 – 7 = 7
… E MUITO MAIS…
MESMO OS NÚMEROS DO PRIMEIRO MEMBRO SENDO DIFERENTES DOS NÚMEROS USADOS NO SEGUNDO MEMBRO, ELES APRESENTAM O MESMO RESULTADO, PROVANDO QUE SÃO EQUIVALENTES E SE ENQUADRAM NA RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS.
OBSERVE AS IMAGENS A SEGUIR


INTUITIVAMENTE AS PESSOAS, ESPECIALMENTE DO NORDESTE DO BRASIL QUE NÃO POSSUEM ÁGUA PRÓXIMO ÀS SUAS CASAS, USAM DESTE ARTIFÍCIO PARA BUSCAREM ÁGUA EM LONGAS DISTÂNCIAS E COLOCAM A MESMA QUANTIDADE DE LÍQUIDO EM AMBOS OS BALDES.
VEJA QUE MESMO NO SEGUNDO EXEMPLO QUE TEMOS DOIS BALDES DE UM LADO E UM OUTRO BALDE DO OUTRO, PERMANECE A EQUIVALÊNCIA, OU SEJA A RELAÇÃO DE IGUALMENTE ENTRE OS DOIS MEMBROS, OU BALDES DO LADO ESQUERDO E BALDE MAIOR DO LADO DIREITO, MANTENDO-SE O EQUILÍBRIO OBTIDO PELA MESMA QUANTIDADE (ÁGUA), OU MESMO PESO.
AGORA, VAMOS AVANÇAR UM POUCO MAIS.
E SE FOR ADICIONADO NO SEGUNDO MEMBRO UM NÚMERO QUALQUER, SERÁ QUE FICA MANTIDA A EQUIVALÊNCIA? VAMOS VER!
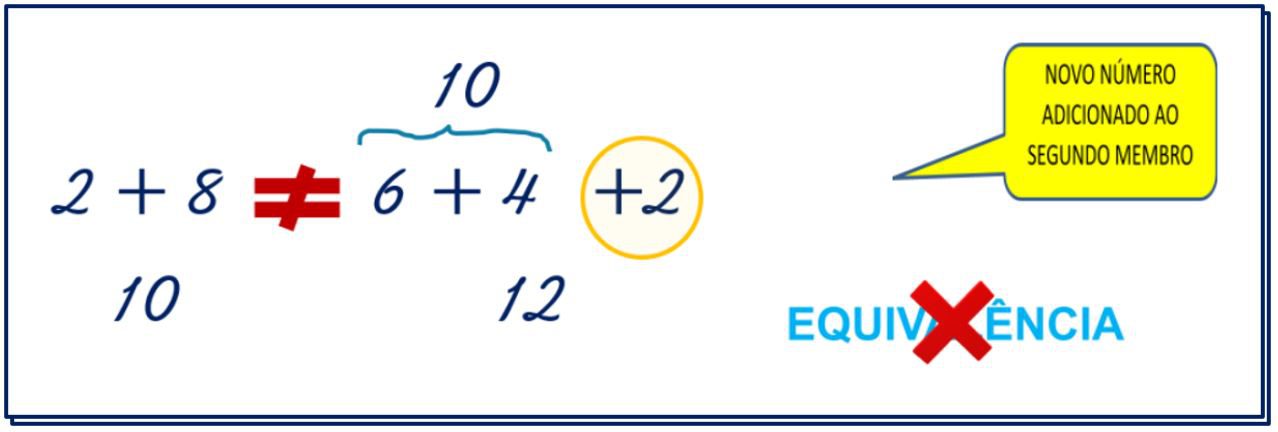
UTILIZANDO O PRIMEIRO EXEMPLO, NO CASO DA ADIÇÃO, ACRESCENTAMOS DUAS UNIDADES NO SEGUNDO MEMBRO: (6 + 4) + 2, SABEMOS QUE 6 + 4 = 10 E 10 + 2 = 12. NO PRIMEIRO MEMBRO O RESULTADO DE 2 + 8 = 10, ENTÃO, FICA CLARO QUE AO ADICIONAR UM OUTRO NÚMERO EM APENAS EM UM DOS MEMBROS, PERDE-SE A EQUIVALÊNCIA, OU SEJA, O RESULTADO DA ADIÇÃO NO PRIMEIRO MEMBRO É DIFERENTE DO RESULTADO DA ADIÇÃO NO SEGUNDO MEMBRO, VEJA QUE USAMOS O SINAL MATEMÁTICO QUE INFORMA ESTA DIFERENÇA ( ≠ ).
MAS SE EU ACRESCENTAR AS DUAS UNIDADES TANTO NO PRIMEIRO MEMBRO QUANTO NO SEGUNDO, VAMOS VER COMO FICA:
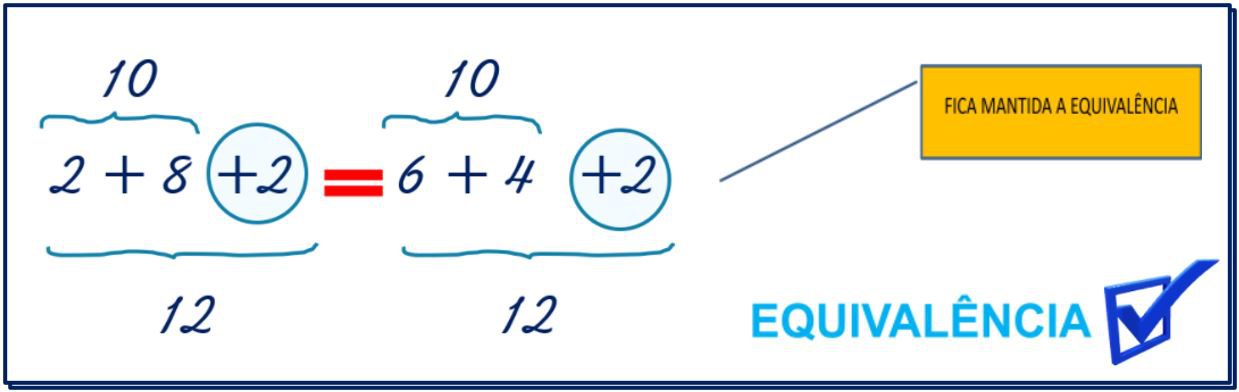
NO PRIMEIRO MEMBRO TEMOS ENTÃO AGORA (2 + 8) + 2, SABEMOS QUE 2+8=10 E 10 + 2 = 12, MANTENDO ASSIM A EQUIVALÊNCIA COM O RESULTADO DO SEGUNDO MEMBRO QUE TAMBÉM É 12.

E ISSO QUE ACONTECE QUANDO VAMOS À FEIRA E ENCONTRAMOS AQUELAS VELHAS BALANÇAS COM DOIS PRATOS E ALGUNS PESOS, COMO NA IMAGEM NO INÍCIO DA NOSSA AULA DE HOJE. ORA, ORA, ELAS SE BASEIAM NA PROPRIEDADE DE EQUIVALÊNCIA. O CLIENTE ESCOLHE SUA MERCADORIA, E O FEIRANTE COLOCA EM UM PRATO DA BALANÇA E BUSCA O EQUILÍBRIO POR MEIO DE VÁRIOS PESOS, DE UM A CINCO QUILOS OU MAIS E TAMBÉM MENOS, ATÉ PESOS EM GRAMAS PARA TER MAIOR PRECISÃO NO VALOR A SER COBRADO. E GERALMENTE ELE DIZ ASSIM: “__ PEGA MAIS DOIS TOMATES PRA DAR UM QUILO”. NÃO É MESMO!
E SERÁ QUE ISSO VALE TAMBÉM PARA A SUBTRAÇÃO? VAMOS PEGAR O EXEMPLO ANTERIOR:

JÁ VIMOS QUE 7 – 2 = 5 (NO PRIMEIRO MEMBRO). ADICIONAMOS DUAS UNIDADES NO SEGUNDO MEMBRO, FICANDO (9 – 4) + 2. ORA, SABEMOS QUE 9 – 4 = 5 E 5 + 2 = 7. FICA AÍ REGISTRADO QUE O RESULTADO DO PRIMEIRO MEMBRO É DIFERENTE DO SEGUNDO MEMBRO.
AGORA, VAMOS TAMBÉM REPETIR O EXEMPLO DA ADIÇÃO ADICIONAR IGUALMENTE MAIS DUAS UNIDADES TAMBÉM NO PRIMEIRO MEMBRO.

E VOCÊ PODE PENSAR EM OUTRO NÚMERO DIFERENTE DE 2, E PODE SER ATÉ OPERAÇÕES DIFERENTES TAMBÉM, MULTIPLICAÇÃO OU DIVISÃO.
QUANDO AS PESSOAS, NA ÍNDIA OU NO NOSSO NORDESTE BRASILEIRO VÃO BUSCAR ÁGUA NO POÇO DISTANTE, COLOCAM UM JUGO NOS OMBROS E EQUILIBRAM DOIS BALDES COM A MESMA QUANTIDADE DE ÁGUA. ISSO FACILITA PARA CARREGAR, DANDO EQUILÍBRIO TAMBÉM AO CORPO QUE FAZ FORÇAS IGUAIS DO LADO DIREITO E DO LADO ESQUERDO.

AH, UMA DICA BEM ESPECIAL PARA QUEM USA BOLSA OU MOCHILA. BUSQUEM COLOCAR O MÍNIMO DE PESO POSSÍVEL PORQUE SENÃO VOCÊ PODE CAUSAR DANOS À SUA COLUNA POIS SE VOCÊ TEM O HÁBITO DE CARREGAR A BOLSA OU MOCHILA SÓ DE UM LADO, A EQUIVALÊNCIA NÃO É MANTIDA, OU SEJA, O PESO DA DIREITO NÃO É IGUAL AO DA ESQUERDA OU VICE-VERSA E ISSO PODE TRAZER CONSEQUÊNCIAS À SUA COLUNA VERTEBRAL.
ESPERO QUE TENHA GOSTADO DE NOSSA AULA HOJE.
ENTENDEU TUDO?
ESPERO QUE SIM.
VIMOS QUE A RELAÇÃO DE IGUALDADE ENTRE DOIS MEMBROS ESTÁ MESMO NO NOSSO DIA-A-DIA!!
| Referências – Texto elaborado com fins pedagógicos. | https://portal.educacao.go.gov.br/fundamental/aula-2-matematica-5o-ano-2o-corte/https://www.youtube.com/watch?v=4N16kmPRsRI (Khan Academy) |
| Objetivos de Aprendizagem e Desenvolvimento | (EAJAMA0410) Compreender que a relação de igualdade existente entre dois membros permanece ao adicionar, subtrair, multiplicar ou dividir cada um desses membros por um mesmo número, para construir a noção de equivalência. |
Professor, essa aula segue a Matriz Estruturante para a Eaja 2021. Foi elaborada no ano de 2020, com a suspensão das aulas presenciais devido a pandemia da Covid-19 e segue as orientações de flexibilização curricular para o biênio 2020/2021 (Ofício Circular 149/2020 Dirped).

