Olá, educando (a)! Esta videoaula de Matemática foi veiculada na TV no dia 04/03/2021 (quinta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.

Nesta atividade, você, estudante do 9º ano, irá identificar e reconhecer um número racional e um número irracional, estabelecendo relações quando um número decimal é uma dízima periódica, reconhecendo e desenvolvendo procedimentos necessários para determinar sua fração geratriz, ou processo contrário. Você, também, poderá classificar as dízimas periódicas em períodos simples ou composto.
E aí, estão preparados?
Então pegue o seu material, tenha bastante atenção e não fique fora desta videoaula!!!!!
Assista a videoaula a seguir, com a temática: Números racionais: dízimas periódicas e frações geratrizes
Olá, nesta atividade, você irá compreender a organização de dois conjuntos numéricos muito importantes: os números racionais (Q) e os números irracionais (I). Para iniciar os estudos, procure relembrar o que são números racionais, representados pela letra Q.
Abaixo, tem-se uma definição desses números:
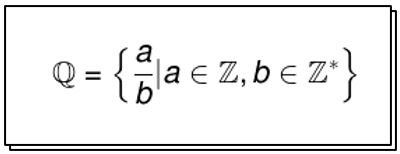
A definição explícita que os números racionais podem ser qualquer número que possa ser representado na forma de uma fração, sendo obrigatoriamente o numerador e denominador serem números inteiros, onde o denominador sempre diferente de zero.
No ano escolar anterior (8º ano) você deve ter realizado inúmeras transformações de frações em números decimais e transformações de números decimais em frações. Para relembrar essas estratégias de transformação, acompanhe atentamente as informações abaixo:
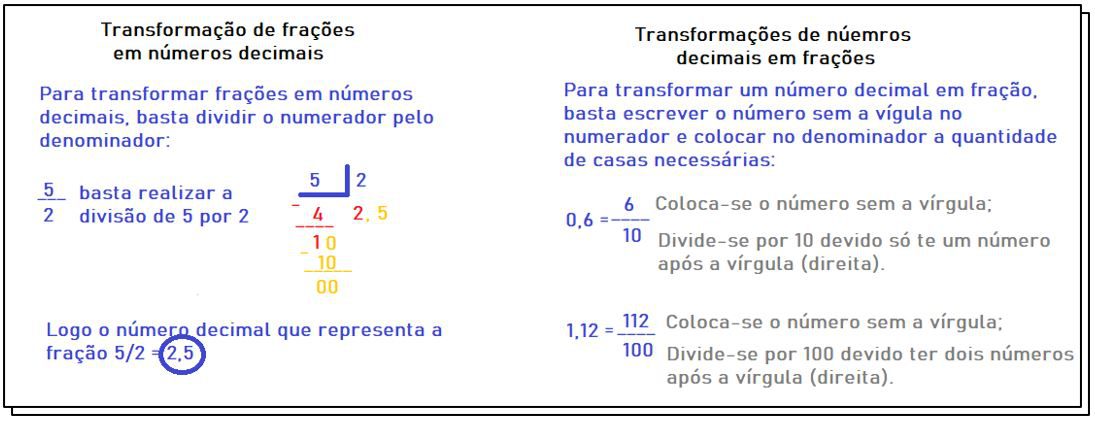
Um fator muito importante a se destacar é quando tem-se um número decimal infinito, como por exemplo:
0,3333…
1,4444…
2,35555…
Estes números decimais infinitos são chamados de dízimas periódicas, que, recebem esse nome “periódicas” por conter um período numérico que se repete ao infinito. Por exemplo:
0,333… o período é 3, pois é este número que se repete infinitas vezes;
1,444… o período é 4, pois é este o número que se repete infinitas vezes;
0,232323… período 23, pois é este o número que se repete infinitas vezes;
As dízimas apresentadas acima, indicam dízimas periódicas simples, pois após a vírgula já se encontra o número que se repete infinitas vezes. Pode acontecer, também, de haver dízimas periódicas compostas, quando o período da dízima não está logo após a vírgula, neste caso, tem-se o que chamamos de “anteperíodo” e é ele que determina quando uma dízima periódica é composta. Veja os exemplos:
2,3555… o período é 5, pois é este o número que se repete infinitas vezes, além de ter um “anteperíodo” 3, que é um número que está após a vírgula e antecede o período.
1,2343434… período 34, pois é este o número que se repete infinitas vezes, tendo como anteperíodo o número 2.
Transformando uma dízima periódica simples em uma fração geratriz
A fração geratriz é uma fração que ao dividir o numerador pelo denominador encontra-se uma dízima periódica. No exemplo abaixo, você poderá acompanhar esse processo de transformação de uma dízima periódica simples em uma fração geratriz. Para isso acompanhe o método algébrico:
Deseja-se transformar o número 0,3333… em uma fração geratriz:

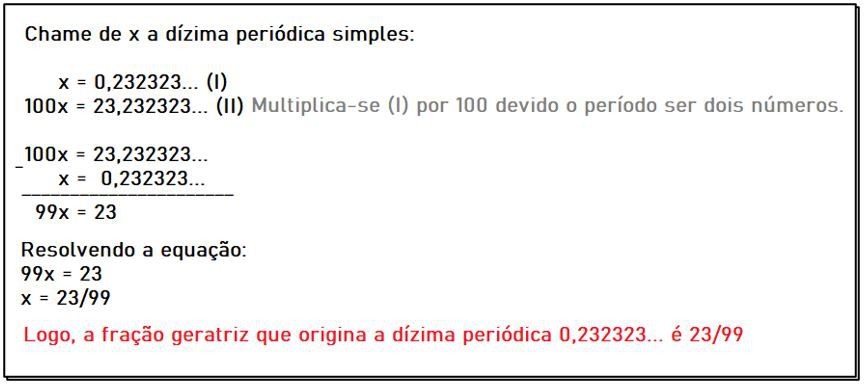
Para se apropriar ainda mais do método algébrico de transformações de dízimas periódicas simples em uma fração geratriz, observe e analise o exemplo a seguir:
Toma-se a dízima periódica simples: 0,232323…
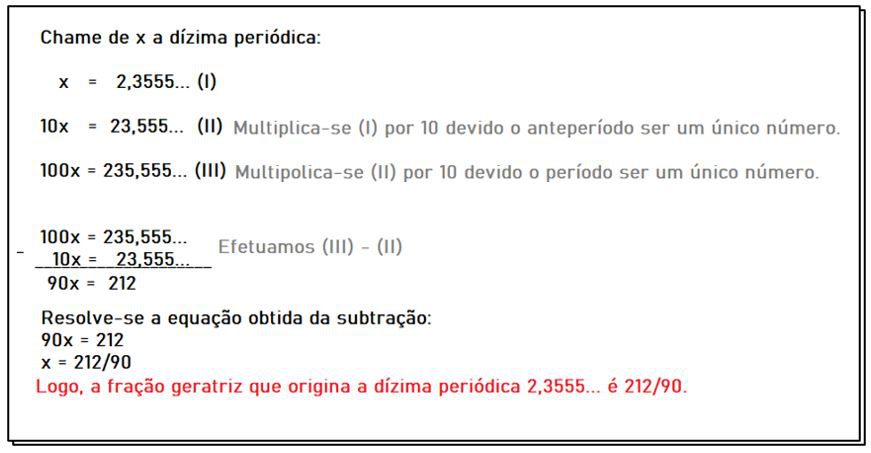
Agora veja um exemplo de transformação, quando se tem um anteperíodo, ou seja, quando a dízima periódica é composta:
Toma-se a dízima periódica 2,3555…
Viu como é fácil transformar uma dízima periódica em uma fração geratriz!
Agora é com você, resolva as situações abaixo:
Questão 01. Classifique as dízimas periódicas em simples ou compostas:
a) 1,333… = __________________________________________________
b) 2,444… = __________________________________________________
c) 1,3444… = _________________________________________________
d) 0,232323… = ______________________________________________
e) 45,8888… = ________________________________________________
Questão 02. Transforme as dízimas periódicas em frações.
a) 0,6666… = _________________________________________________
b) 1,8888…= _________________________________________________
c) 2,4333…= __________________________________________________
Agora, continuando a sequência de estudos, observe a definição dos números irracionais (I):
O conjunto dos números irracionais (I) pertencem ao conjunto dos números decimais infinitos e aperiódicos (que não possuem período), ou seja, números que não podem ser representados na forma de frações. Exemplos:
- Todas as raízes não exatas geram um número que não pode ser escrito na forma de fração, devido o seu número decimal não se tratar de uma dízima periódica, já que não há um número que se repete ao infinito, observe:
√2 = 1,414213562373….
√3 = 1,732050807568….
√5 = 2,236067977499…
√7 = 2,645751311064…
- “O número pi (π) é o mais famoso dos números irracionais transcendentes. Seu valor é π = 3,14159265358979323846… e representa a proporção da medida da circunferência e do seu diâmetro.
- Um outro exemplo de irracional transcendente é o número de Neper, representado por e, sendo aproximadamente igual a 2,718281…
- Podemos ainda citar o número de ouro, representado por Phi (ϕ). Seu valor é ϕ = 1,618033… O número de ouro é encontrado a partir da razão áurea ou divina proporção, sendo encontrada em muitos elementos da natureza. Além disso, esta razão está presente em diversas pinturas, esculturas e construções.” Fonte: https://www.todamateria.com.br/numeros-irracionais/
Chegou a hora de pôr em prática esses estudos:
Questão 03. Observe atentamente os números abaixo, e identifique se eles são números racionais ou irracionais.
a) 2,345555… = ______________________________________________
b) 7,8888… = _________________________________________________
c) 1,3456897654678321… = __________________________________
d) 1,33333… = ________________________________________________
Para finalizar a atividade, e, consequentemente, exercer uma síntese dos estudos propostos nela, observe o exemplo de uma situação que envolve as operações com números racionais.

Questão 04. Resolva a expressão numérica, explicando cada um de seus “passos” de resolução, conforme foi realizando no exemplo anterior:
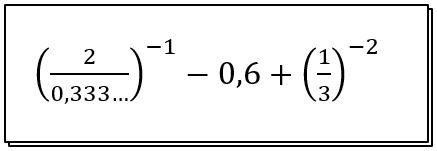
Em síntese, nesta atividade você pôde (re)lembrar o conjunto numérico dos números racionais (Q), percebendo as aplicações usuais dos números inteiros em nossa sociedade e também algumas operações de transformações com os números racionais, além de perceber as operações matemáticas básicas com esses números. As questões propostas puderam auxiliar a sua produção matemática dos conceitos estudados, viabilizando o exercício contínuo do fazer e pensar matematicamente. Até a próxima atividade e não se esqueça de revisar todo o conteúdo.
Para saber mais sobre as dízimas periódicas, assista ao vídeo:
“O que São Dízimas Periódicas Simples e Composta – Estatística Interativa #29” – Canal: Estatística Interativa – Link: https://www.youtube.com/watch?v=ZZntGbeG19c
Para saber mais sobre os números irracionais, assista ao vídeo:
Prof Laís – Matemática – Link: https://www.youtube.com/watch?v=T1cz3oSbYes
| Referências – Texto elaborado com fins pedagógicos. | https://www.todamateria.com.br/numeros-irracionais/ |
| Habilidades | Habilidades Estruturantes (EF08MA05-A) Reconhecer e utilizar procedimentos para obtenção de uma fração geratriz para uma dízima periódica simples. (EF09MA02-A) Reconhecer um número racional como um número real, cuja representação decimal é finita ou decimal infinita e periódica (dízima periódica) e que pode ser escrita em forma de fração irredutível a/b, com b diferente de zero. (EF09MA02-C) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica em situações diversas. Habilidades Complementares EF09MA01 AEF09MA02-B |
