Olá, educando (a)! Esta videoaula de Matemática foi veiculada na TV no dia 03/03/2021 (quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Nesta atividade, você, estudante do 8º ano, irá estudar sobre as operações de adição, subtração, multiplicação, divisão, potenciação e radiciação dos números racionais, compreendendo os esquemas de transformações de dízimas periódicas em frações geratrizes.
Assista a videoaula a seguir, com a temática: Operações com números racionais e notação científica
Olá, nesta atividade você terá a oportunidade de estudar sobre as operações matemáticas com os números inteiros e racionais. Para iniciar os estudos é necessário definir primeiramente o conjunto dos números inteiros, definidos pela letra Z.
Z = {…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …}
Pode-se notar que o conjunto dos números inteiros (Z) começam no menos infinito, e vai se aproximando do zero, após o zero, tem-se os números inteiros positivos até o infinito. Assim, o conjunto dos números inteiros apresentam dois infinitos: um negativo e outro positivo. É importante notar, também, que este conjunto numérico possui um número central que é o zero.
Os números inteiros tem grande importância nas relações humanas sociais, sobretudo as de ordem financeira, quando se deseja representar saldos positivos ou negativos, além disso, podem ser utilizados em diversos contextos, como: medidas de temperatura, fusos horários, nivelamento territorial em relação ao nível do mar, entre outros.
Veja alguns exemplos de situações contextuais em que utilizam-se os números inteiros:
Na Espanha, haverá uma corrida de Fórmula 1 às 17 horas. Qual o horário em que uma pessoa deve ligar a televisão, aqui no Brasil, se ela está a quatro fusos horários a oeste da Espanha?
Resolução:
Se a pessoa está a oeste, significa que está atrasada em relação ao horário do evento, ou seja, -4 horas, pois cada fuso corresponde a uma hora.
Assim, a diferença será de 4 horas.
17 h – 4 h = 13 horas
Então, a pessoa no Brasil deve ligar a televisão às 13 horas.
Outro conjunto de grande importância, são os números racionais, que é representado pela letra Q e é definido como:

Ou seja, o conjunto dos números racionais pode ser representado por qualquer número na forma de fração, desde que, seu numerador (número de cima da fração) seja um número inteiro e o seu denominador (número de baixo da fração) seja qualquer número inteiro, excluindo-se a possibilidade de colocar o zero. Assim, o conjunto dos números racionais (Q) pode ser qualquer número em que se pode representar na forma de fração.
É importante lembrar que qualquer número inteiro, também é um número racional, pois eles podem ser representados na forma de fração. Observe:

Assim, todos os números inteiros também fazem parte dos números racionais, pois todos eles podem ser representados em diversas formas de frações. Então os números racionais são compostos por todos os números inteiros acrescidos dos números decimais e frações que não se transformam em números inteiros.
Toma-se como exemplo, os seguintes números racionais:

Uma característica muito importante dos números racionais é que eles podem ser colocados na reta numérica, observe:
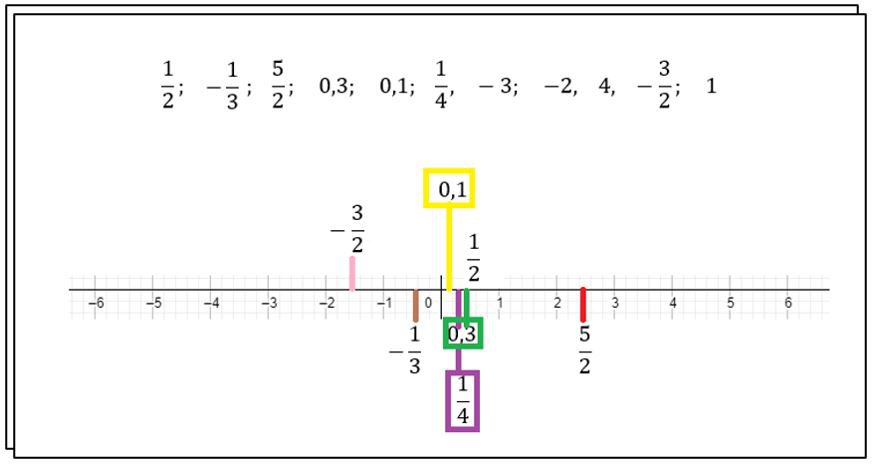
Na reta numérica todo número escrito na forma de fração ou em forma decimal (representado com vírgula, indicando um número não inteiro).
Uma característica bem interessante dos números racionais é a sua capacidade de representação na forma decimal ou na forma de fração.
Para compreender melhor sobre essas transformações, inicia-se o estudo das “Transformações das frações em números decimais”. Observe:

ara transformar qualquer fração em número decimal, é necessário dividir o numerador pelo denominador, obtendo como resposta o número decimal que representa a fração.
Agora, observe “Transformações dos números decimais em frações”:

Viu como é fácil transformar um número decimal em fração?
Agora é com você, resolva as questões 01 e 02 envolvendo as transformações de fração em decimal e decimal em fração.
Questão 01. Faça as transformações dos números fracionários em números decimais:
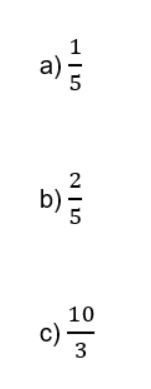
Questão 02. Faça as transformações dos números decimais em números fracionários:
a) 0,4
b) 5,3
c) 2,98
As frações e números decimais, também, podem expressar um conceito muito importante dentro da matemática que são as porcentagens. Como o próprio nome sugere, as porcentagens é um índice que se refere a 100, ou seja, mantém relação direta com esse parâmetro de 100. Observe alguns exemplos de transformação de frações e/ou números decimais em porcentagens:

Agora é com você!
Questão 03. Indique qual a porcentagem que cada um dos números decimais ou fracionários estão indicando:
a) 0,3
b) 0,03
c) 1,2
d) 1/2
Questão 04. Resolva as situações abaixo envolvendo porcentagens, siga o exemplo proposto na alternativa a.
a) Exemplo:

b) Um tênis que custa R$ 150,00 está com desconto de 20%. Qual o novo valor do tênis com desconto?
c) Um computador antes da pandemia custava R$ 2 000,00 durante a pandemia, ele teve um aumento de 60%. Calcule o valor atualizado do computador após o aumento.
Em síntese, nesta atividade você teve a possibilidade de estudar sobre dois conjuntos numéricos: números inteiros e números racionais. Com os números inteiros, você percebeu os seus dois infinitos, um positivo e outro negativo, acompanhando um exemplo de aplicação contextual dos conceitos envolvendo os números inteiros. Já os números racionais, você percebeu que representa qualquer número que pode ser escrito na forma de fração, neste caso, percebeu que todos os números inteiros fazem parte do conjunto dos números racionais. Além disso, por meio da visualização da reta, pôde perceber que os números racionais podem ser facilmente colocados na reta numérica, e, que eles podem ser inteiros, fracionários ou decimais, estudando alguns métodos de transformação de decimal para fração e fração para decimal. Finalizando esta atividade, você percebeu que os números racionais também podem expressar porcentagens, e que estas são muito úteis em nossas relações financeiras. Até a próxima atividade e não se esqueça de revisar os conteúdos estudados. Até lá!
Para saber mais sobre os números inteiros e racionais, assista ao vídeo:
Para saber mais sobre porcentagens e sua aplicabilidade, assista ao vídeo:
| Habilidades | Habilidades Estruturantes (EF07MA04-A) Ler, interpretar e resolver problemas que envolvam operações com números inteiros. (EF07MA11-B) Ler, interpretar, resolver, analisar e elaborar problemas com adição, subtração, multiplicação, divisão, potenciação e radiciação de números racionais, a relação entre elas e suas propriedades operatórias em situações diversas como o uso de escalas em mapas, o uso de representações de decimais exatos, porcentagens e dízimas periódicas, entre outros. Habilidade complementar EF08MA01-A |