Esta proposta de atividade de MATEMÁTICA é destinada aos estudantes do 6° Período (8ª Série) da Educação de Jovens e Adultos – EJA
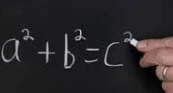
O Teorema de Pitágoras
O Teorema de Pitágoras é uma ferramenta matemática que tem diversas aplicações práticas em cálculos que envolvem triângulos retângulos (aqueles que possuem um ângulo de 90°).
Imagem: canva.com/teorema_de_Pitágoras
Onde se aplica o Teorema de Pitágoras?
A principal aplicação do Teorema de Pitágoras está no cálculo de comprimentos de lados desconhecidos em triângulos retângulos e, consequentemente, determinar diagonais de retângulos.
Enunciado do Teorema de Pitágoras
O Teorema de Pitágoras afirma que em um triângulo retângulo:
“O quadrado do maior lado, do triângulo (hipotenusa) é igual a soma dos quadrados dos outros dois lados (os catetos)”.
Veja a figura:
Imagem: canva.com/triângulo retângulo
Situações Problema
Problema 1
Um chacareiro está construindo uma porteira para o seu curral. A porteira é retangular e tem madeira na horizontal, vertical e uma na diagonal para dar mais firmeza. A madeira na vertical mede 6m e a horizontal mede 8m. Ele precisa determinar o comprimento da terceira madeira, que vai diagonalmente entre as outras duas e formará a parte inclinada da porteira. Ajude o chacareiro! Qual deve ser o comprimento dessa madeira?
Veja a ilustração desse problema:
Imagem: canva.com/porteira
Aplicando o Teorema de Pitágoras.
Observe que as madeiras na vertical, na horizontal e na diagonal, formam um triângulo retângulo. Considerando x a medida da madeira na diagonal, podemos afirmar que o quadrado dessa medida é igual a soma dos quadrados das outras medidas, ou seja:
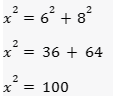
Extraindo a raiz quadrada, obtemos 10 metros, a medida da madeira.
Problema 2
Um bombeiro precisa resgatar uma pessoa que está presa em um prédio em chamas. A pessoa está em um andar superior, a uma altura de 15m do solo. Para planejar o resgate, o bombeiro vai posicionar a escada a 8m de distância do prédio de modo a alcançar a janela do andar onde a pessoa está. Qual deverá ser a medida dessa escada para que ele possa resgatar essa pessoa?
Veja a ilustração:
Imagem: canva.com/escada_prédio_bombeiro
Temos, claramente, um triângulo retângulo onde a escada é o maior lado (hipotenusa), a altura do prédio e a distância do pé da escada ao prédio são os catetos, aplicando o Teorema de Pitágoras, teremos:
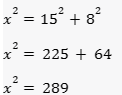
Extraindo a raiz quadrada, obtemos 17 metros, a medida do comprimento da escada.
Ficamos por aqui, até o próximo.
Atividade
QUESTÃO 01
Paulo, infelizmente, em um momento complicado no trânsito, se chocou com um poste quebrando-o (veja a figura). Agora ele precisa comprar outro para repor o que foi danificado. O valor do poste é de acordo com o seu comprimento. Ajude Paulo a determinar essa medida.
canva.com.br/motos e postes
QUESTÃO 02
Clara estava brincando de jogar bola com seus amigos e em determinado momento sua bola foi parar na copa de uma árvore. Ela então pediu ajuda para os colegas, colocaram uma escada junto à árvore para alcançar a bola. Sabendo que a bola estava a 8 metros do chão e o pé da escada (base) estava posicionada a 6 metros da árvore (veja a figura), qual o comprimento da escada utilizada para alcançar a bola?
canva.com.br/árvore_escada_menina
QUESTÃO 03
Um nadador parte da beira de um lago e nada 30 metros em linha reta até uma boia. Ele então vira à direita, sob um ângulo de 90°, e nada mais 40 metros até chegar a uma praia. Podemos afirmar que a distância direta entre o ponto de partida do nadador e a praia é
(A) 50 metros.
(B) 70 metros.
(C) 58 metros.
(D) 40 metros.
QUESTÃO 04
Uma escada de 5 metros de comprimento está apoiada em uma parede vertical. A base da escada está a 3 metros de distância da parede. Podemos afirmar que a altura da parede até onde a escada alcança é
(A) 4 metros.
(B) 2 metros.
(C) 3 metros.
(D) 1 metro.
SAIBA MAIS
Assista ao vídeo do canal do professor Hélio no YouTube e tire suas dúvidas sobre o teorema de Pitágoras.
| Autoria | Professor Hélio Roberto da Rocha, Mestre em matemática |
| Componente curricular | Matemática |
| Objetivos de aprendizagem e desenvolvimento | (EAJAMA0827) Interpretar, resolver e elaborar situações-problema de aplicação do teorema de Pitágoras. |
| Referencial Teórico | SOUZA, Joamir Roberto de: Matemática realidade & tecnologia: 6º ano: ensino fundamental: anos finais /Joamir Roberto de Souza. – 1. ed. – São Paulo: FTD, 2018. GIOVANNI JÚNIOR, José Ruy – A conquista da matemática: 6° ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018. PATARO, Patricia Moreno Matemática essencial 6° ano: ensino fundamental, anos finais / Patricia Moreno Pataro, Rodrigo Balestri. – 1. ed. – São Paulo: Scipione, 2018. |
