Olá, educando (a)! Esta videoaula de Matemática para o Agrupamento G (7º ano) do Ciclo da Adolescência foi veiculada na TV no dia 03/08/2021 (Quarta-feira). Aqui no Portal Conexão Escola, ela está disponível juntamente com a proposta de atividade.
Assista a videoaula a seguir com a temática: Sequências numéricas e proporcionalidade
Nesta atividade de matemática, você estudará sobre os números inteiros, iniciando com:
- Sequências numéricas;
- Resolução geral de uma sequência numérica por meio da álgebra;
- Razão;
- Proporção.
Para iniciar vamos relembrar o que é uma sequência, para então perceber o que são sequências numéricas.
Sequência é uma relação finita ou infinita de elementos que podem ser figuras, números, letras, entre outros. Uma sequência é definida de acordo com seus elementos e com a ordem em que eles aparecem. Veja alguns exemplos.
• (janeiro, fevereiro, março, abril …): sequência dos meses do ano. • (1, 3, 5, 7 …): sequência dos números naturais ímpares.
• (seis, sete, sessenta, sessenta e um …): sequência dos números escritos por extenso cujo nome começa com a letra s.
Cada elemento de uma sequência recebe o nome de termo. Quando uma sequência possui uma regra de formação, ou seja, a obtenção de cada um de seus termos obedece a determinado padrão ou regra, podemos obter os próximos termos. Quando a obtenção de um termo depende de termo(s) anterior(es), ocorre o que chamamos de recorrência ou recursão.
Sequências numéricas
Como já estudamos o assunto sequências numéricas em uma atividade anterior, vamos nos concentrar nas sequências numéricas. Observe as sequências numéricas que geram os múltiplos de um número natural:
Múltiplos de 2: {0, 2, 4, 6, 8, 10, 12, …}
Tomando um número n, como um número natural com início no zero até o infinito, tem-se que a sequência pode ser obtida, algebricamente, por:
2.n
O mesmo pode ser aplicado à qualquer outra sequência que envolve múltiplos de um número natural. Observe:
Múltiplos de 3: {0, 3, 6, 9, 12, 15, 18, …}
obtida por: 3.n
Múltiplos de 5: {0, 5, 10, 15, 20, 25, 30, …}
obtida por: 5.n
Múltiplos de 10: {0, 10, 20, 30, 40, 50, 60, …}
obtida por: 10.n
Agora observe as sequências:
{1, 2, 4, 8, 16, 32, 64, …}
Para indicar essa sequência numérica, repare que é necessário sempre dobrar o termo anterior… dobro de 1 = 2, dobro de 2 = 4, dobro de 4 = 8 e assim por diante. Logo a sentença matemática algébrica que representa essa situação é:
(sendo n um número natural)
Um fato curioso sobre as sequências numéricas que indicam uma relação com as potências é que dividindo qualquer número a partir do segundo termo, pelo anterior, tem-se uma razão que garante o funcionamento e a “lógica” de organização da sequência numérica.
Observe, por exemplo, a sequência numérica obtida a partir das potências de 10.
{1, 10, 100, 1000, 10 000, 100 000, …}
(sendo n um número natural)
Se organizarmos, a divisão de um termo pelo seu antecessor, tem-se o conceito de razão que, por sua vez, é capaz de gerar toda a sequência numérica:
Repare que, em todas essas divisões, o resultado é sempre o mesmo: 10.
Agora que percebemos a relação das sequências numéricas que podem ser representadas por potências, vamos aprofundar nossos estudos sobre o que é uma razão.
Razão
Para compreender o conceito de razão em um contexto social, observe a situação abaixo:
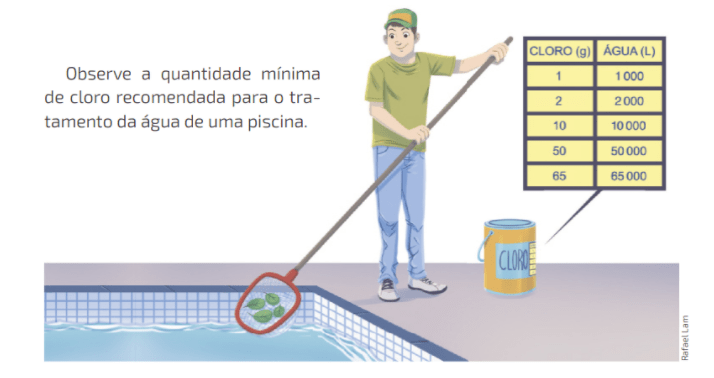
Podemos notar que a quantidade de cloro varia de acordo com a quantidade de água, pois temos 1 g de cloro para 1 000 L de água, 2 g de cloro para 2 000 L de água, e assim por diante. Escrevendo razões para representar as informações do quadro, temos:
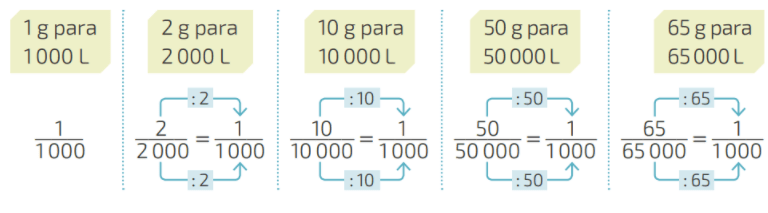
É importante notar aqui, que, se simplificarmos cada uma das razões tem-se, sempre a mesma constante 1:1000, ou seja 0,001. Dizemos que a razão permanece constante, neste caso.
O conceito de razão nos permite fazer comparações entre dois números. Para saber, por exemplo, quantas vezes o número 12 é maior do que o número 6, ou seja, para saber qual é a razão entre 12 e 6, procedemos da seguinte maneira:

Atividade 1
Agora é com você! Coloque em prática o que você estudou resolvendo em seu caderno, as questões a seguir:
Questão 01. Escreva uma razão para representar cada frase.
a) Em um campeonato de vôlei, determinada equipe venceu 8 dos 13 jogos que disputou.
b) Para preparar certo bolo são necessários 60 g de açúcar para cada 100 g de farinha.
Questão 02. Ana está poupando dinheiro para fazer uma viagem. A cada R$ 10,00 que ganha, ela poupa R$ 3,00 .
a) Quantos reais Ana poupará se ganhar R$ 400,00?
b) Que razão representa quanto Ana poupa em relação ao que ganha?
Grandezas proporcionais
Em algumas situações, duas ou mais grandezas podem estar relacionadas e essa relação pode ser de proporcionalidade direta ou de proporcionalidade inversa.
Agora, vamos estudar, por meio de alguns exemplos, o que são grandezas diretamente proporcionais e grandezas inversamente proporcionais.
Grandezas diretamente proporcionais

Podemos notar que, de 1 kg para 4 kg, a medida da massa das laranjas foi multiplicada por 4. Como o preço a ser pago pelas laranjas está diretamente relacionado à sua medida de massa, temos que o preço a ser pago também será multiplicado por 4.
2,65 ⋅ 4 = 10,6
Assim, uma pessoa vai pagar R$ 10,60 por 4 kg de laranja.
Nesse caso, o valor a ser pago depende da medida da massa das laranjas. Se essa medida aumentar 2 vezes, o preço a ser pago também aumentará 2 vezes. Se essa medida diminuir pela metade, o preço a ser pago também diminuirá pela metade, e assim por diante. Dessa maneira, dizemos que a medida da massa das laranjas e o preço a ser pago são grandezas diretamente proporcionais.
Na situação das laranjas, podemos formular uma sentença algébrica que determina o valor a ser pago pelas laranjas em função da quantidade de quilos que um cliente pode comprar. Atribuímos a fórmula:
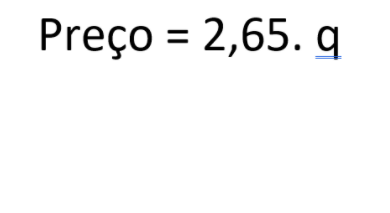
Grandezas inversamente proporcionais
Para colher o milho que plantou, Francisco utilizará duas colheitadeiras que, juntas, vão colher toda a plantação em 6 dias. Se Francisco decidir utilizar 6 colheitadeiras, em quantos dias, mantendo o ritmo de trabalho, será feita toda a colheita?
Para responder a essa questão, observe o seguinte esquema.

Observando o esquema, podemos notar que, de duas para seis, a quantidade de colheitadeiras foi multiplicada por 3. Nesse caso, como as colheitadeiras vão manter o ritmo de trabalho, a medida do tempo gasto para fazer a colheita será reduzida à terça parte, ou seja, será dividida por 3.
6 : 3 = 2
Assim, se Francisco utilizar 6 colheitadeiras, a colheita será realizada em dois dias.
Nesse caso, a medida do tempo de colheita depende da quantidade de colheitadeiras. Se a quantidade de colheitadeiras dobrar, a medida do tempo de colheita será diminuída pela metade. Se a quantidade de colheitadeiras diminuir pela metade, a medida do tempo de colheita será o dobro, e assim por diante. Logo, se Francisco utilizar apenas uma colheitadeira, a colheita será feita em 12 dias.
Dessa maneira, dizemos que a quantidade de colheitadeiras e a medida do tempo da colheita são grandezas inversamente proporcionais.
Veja, em cada linha do esquema, que, se multiplicarmos a quantidade de colheitadeiras pela medida do tempo de colheita, obteremos 12 como resultado.

De acordo com essa situação, e sabendo em quantos dias a colheita será realizada se apenas uma colheitadeira for utilizada, podemos escrever uma fórmula para calcular a medida de tempo de colheita em relação à quantidade de colheitadeiras.

Viu como é fácil compreender as grandezas inversamente proporcionais? Basta pensar inversamente ao que está sendo proposto.
Para elucidar melhor as grandezas inversamente proporcionais, acompanhe os exemplos resolvidos abaixo:
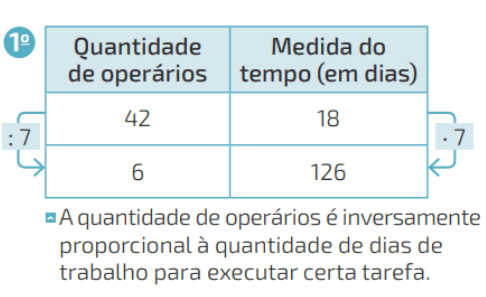
Exemplo 01. Para construir um edifício em 18 dias são necessários 42 operários. Com a crise financeira, o dono da obra só tem capacidade de trabalhar com 6 operários. Assim, quantos dias serão necessários para que o edifício fique pronto?
Podemos montar uma proporção com duas razões:
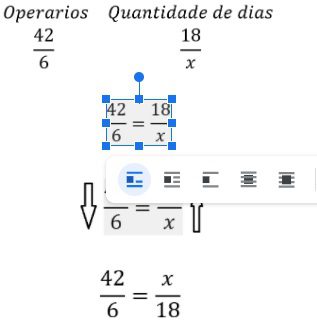
Logo:
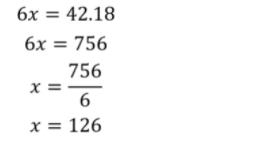
Outra forma de analisar o problema é verificar se o número é múltiplo um do outro, e, assim determinar inversamente a operação:
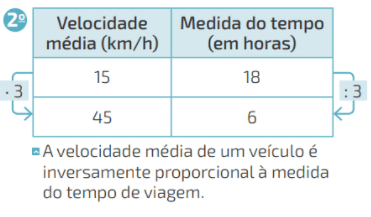
Exemplo 02. Uma bicicleta com velocidade constante de 15 km por hora chega ao seu destino em 18 horas. No entanto, se o ciclista aumentar a velocidade para 45 km por hora, qual deverá ser o tempo de sua chegada, considerando o mesmo destino?
Podemos resolver o problema, novamente por meio da proporção:
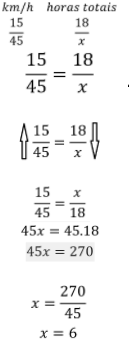
Novamente podemos, também, realizar os cálculos por meio da tabela de proporcionalidade:
Atividade 2
Agora é com você, resolva em seu caderno, as questões abaixo:
Questão 03. Verifique em cada item se as grandezas são proporcionais.
a) A medida da altura de Aline aos 13 anos de idade era 1,55 m e aos 26 anos, 1,76 m. Nesse caso, as grandezas “idade” e “altura” são proporcionais?
b) Em certa fábrica, uma máquina produz 188 peças em 4 h e 94 peças em 2 h de funcionamento. Nesse caso, as grandezas “quantidade de peças produzidas” e a “medida do tempo de funcionamento” são proporcionais?
c) Em um supermercado, o preço do pacote de arroz de 1 kg de certa marca custa R$ 3,70 e o de 5 kg, R$ 17,20. Nesse caso, as grandezas “massa” e “preço” são proporcionais?
Questão 04. . Marcos, Bete e Raul fizeram juntos um investimento de R$ 3 000,00 . Marcos aplicou R$ 500,00, Bete, R$ 1 000,00e Raul, R$ 1 500,00 . Após certo período, esse investimento rendeu R$ 600,00, que eles dividiram em partes diretamente proporcionais às quantias aplicadas. Para calcular quantos reais Raul recebeu de rendimento, podemos construir o seguinte esquema:
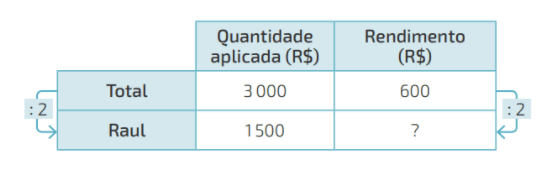
Assim, segue que:
600 : 2 = 300
Portanto, Raul recebeu R$ 300,00 do rendimento. Agora, determine quantos reais de rendimento recebeu cada um dos outros investidores.
Questão 05. Observe a tirinha abaixo:

a) Por que um dos personagens pediu contas separadas?
b) Supondo que o preço de cada prato seja diretamente proporcional à quantidade de alimento nele contida, sugira preços para o menor e para o maior prato.
RELEMBRANDO!
Em síntese, nesta aula você pôde estudar e perceber as sequências numéricas que podem ser geradas por uma fórmula matemática capaz de indicar todos os números da sequência, percebendo, também, que as sequências que são expressas por potenciação, quando dividimos um termo pelo seu anterior, temos a razão da sequência numérica, que por sua vez, pode ser indicada como a relação de divisão entre duas grandezas, grandezas estas que podem ser diretamente proporcionais e inversamente proporcionais. Tais grandezas permeiam o nosso dia-a-dias nas mais diversas situações.
| Referência | PATARO, Patrícia Moreno, BALESTRI, Rodrigo. Matemática essencial 7o ano : ensino fundamental, anos finais Rodrigo Balestri. — 1. ed. — São Paulo : Scipione, 2018. PLND |
| Componente Curricular | Habilidades |
| Matemática | Estruturantes (EF07MA15) Utilizar a simbologia algébrica para expressar regularidades encontradas em sequências numéricas. (EF07MA17-B) Ler, interpretar, resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas. Complementares EF07MA16 EF07MA17-A |

